Chapter 6 Output Feedback

We have presented many algorithms for optimal control of dynamical systems. These algorithms, however, have a strict assumption, i.e., the state of the system is directly available. These controllers are called state-feedback controllers.

In many applications, the state of the system is not readily available but measured via sensors. Therefore, a more realistic model of the dynamical system is \[\begin{equation} \begin{split} \dot{x} &= f(x,u) + w \\ y &= h(x,u) + v \end{split} \tag{6.1} \end{equation}\] where \(x(t) \in \mathbb{X} \subseteq \mathbb{R}^n\) the state of the system, \(u(t) \in \mathbb{U} \subseteq \mathbb{R}^m\) the control (or input), \(y(t) \in \mathbb{Y} \subseteq \mathbb{R}^{d}\) the output (i.e., measurement) of the state and control, and \(f,g\) the evolution and measurement functions (which are sufficiently smooth). \(w(t)\) and \(v(t)\) denote disturbance and measurement noise, respectively. The discrete-time analog of (6.1) is \[\begin{equation} \begin{split} x_{k+1} &= f(x_k,u_k) + w_k \\ y_k &= h(x_k,u_k) + v_k \end{split}, \tag{6.2} \end{equation}\] with \(k\) denoting the discrete timestep. When faced with systems like (6.1) and (6.2), the controller typically needs to use the history of all measurements, also known as output feedback \[ u(t) = \pi(\{y(\tau)\}_{\tau=0}^t), \quad u_k = \pi (\{y_0,\dots,y_k\}). \]

6.1 Least-Squares Estimation

Suppose we are given two random variables \(x \in \mathbb{R}^n\) and \(y \in \mathbb{R}^m\), where \(y\) is a measurement that provides some information about the model \(x\). We are interested in finding an estimator, i.e., a function \(x(y)\), that minimizes \[ \mathbb{E}_{x,y} \left\{ \Vert x - x(y) \Vert^2 \right\}. \] The optimal estimator, \(x^\star(y)\), is called a least-squares estimator: \[ x^\star(y) = \arg\min_{x(\cdot)} \mathbb{E}_{x,y} \left\{ \Vert x - x(y) \Vert^2 \right\}. \] Note that \(x^\star(y)\) is a function with input \(y\). Since \[\begin{equation} \mathbb{E}_{x,y}\left\{ \Vert x - x(y) \Vert^2 \right\} = \mathbb{E}_y \left\{ \mathbb{E}_x \left\{ \Vert x - x(y) \Vert^2 \mid y\right\} \right\}, \tag{6.3} \end{equation}\] it is clear that \(x^\star(y)\) is a least-squares estimator if \(x^\star(y)\) minimizes the conditional expectation in (6.3) for every \(y \in \mathbb{R}^m\), that is, \[\begin{equation} x^\star(y) = \arg\min_{z \in \mathbb{R}^n} \mathbb{E}_x \left\{ \Vert x - z \Vert^2 \mid y \right\}, \quad \forall y \in \mathbb{R}^m. \tag{6.4} \end{equation}\] With this observation, we have the following proposition.

Proposition 6.1 (Least Squares Estimator) The least squares estimator \(x^\star(y)\) is given by \[\begin{equation} x^\star(y) = \mathbb{E}_x \left\{ x \mid y \right\}, \quad \forall y \in \mathbb{R}^m, \tag{6.5} \end{equation}\] i.e., \(x^\star(y)\) returns the conditional mean of \(x\) given \(y\).

Proof. We expand the objective in (6.4) \[ \mathbb{E}_x \left\{ \Vert x - z \Vert^2 \mid y \right\} = \mathbb{E}_x \left\{ \Vert x \Vert^2 \mid y \right\} - 2 z^T \mathbb{E}_x \left\{x \mid y \right\} + \Vert z \Vert^2. \] Observe that problem (6.4) is an unconstrained quadratic optimization, whose optimal solution can be obtained by setting the gradient of objective (w.r.t. \(z\)) to zero: \[ z = \mathbb{E}_x \left\{ x \mid y \right\}, \] concluding the proof.

Depending on the joint distribution of \((x,y)\), the least-squares estimator can be very complicated (due to \(\mathbb{E}_x\left\{ x \mid y\right\}\) being complicated) and in general does not admit a clean solution. We now turn to the family of linear estimators.

6.1.1 Linear Least-Squares Estimation

A linear estimator \(x(y)\) takes the following form \[ x(y) = Ay + b, \quad A \in \mathbb{R}^{n \times m}, b \in \mathbb{R}^n. \] The optimal linear estimator \[\begin{equation} (A^\star, b^\star) = \arg\min_{A,b} \mathbb{E}_{x,y} \left\{ \Vert x - Ay - b \Vert^2 \right\} \tag{6.6} \end{equation}\] is called a linear least-squares estimator.

In the special case where \(x\) and \(y\) are jointly Gaussian random variables, the conditional expectation \(\mathbb{E}_{x} \{x \mid y \}\) is indeed linear, and hence a linear least-squares estimator is also the true least-squares estimator.

Proposition 6.2 (Linear Least-Squares Estimator) If the random variables \((x,y)\) are jointly Gaussian, then the conditional expectation \(\mathbb{E}_x \{x \mid y \}\) is linear in \(y\). Therefore, the linear least-squares estimator (6.6) is also the least-squares estimator.

Now let us turn to characterize the linear least-squares estimator.

Proposition 6.3 (Solution of Linear Least-Squares Estimator) Let \(x,y\) be random variables in \(\mathbb{R}^n\) and \(\mathbb{R}^m\) drawn from some underlying distribution. The means and covariances of \(x\) and \(y\) are given by \[\begin{equation} \begin{split} \mathbb{E}\{ x\} = \bar{x}, \quad \mathbb{E} \{ y \} = \bar{y}. \\ \mathbb{E}\{ (x - \bar{x})(x - \bar{x})^T \} = \Sigma_{xx}, \quad \mathbb{E}\{ (y - \bar{y})(y-\bar{y})^T \} = \Sigma_{yy}, \\ \mathbb{E}\{ (x - \bar{x})(y - \bar{y})^T \} = \Sigma_{xy}, \quad \mathbb{E}\{ (y - \bar{y})(x - \bar{x})^T \} = \Sigma^T_{xy}, \end{split} \end{equation}\] and assume \(\Sigma_{yy}\) is invertible (positive definite). Then the linear least-squares estimator \(x^\star(y)\), i.e., solution of (6.6), is given by \[\begin{equation} x^\star(y) = \bar{x} + \Sigma_{xy} \Sigma^{-1}_{yy} (y - \bar{y}). \tag{6.7} \end{equation}\] The corresponding error covariance matrix is given by \[\begin{equation} \mathbb{E}_{x,y} \left\{ (x - x^\star(y))(x - x^\star(y))^T \right\} = \Sigma_{xx} - \Sigma_{xy} \Sigma^{-1}_{yy} \Sigma^T_{xy}. \tag{6.8} \end{equation}\]

Proof. Problem (6.6) is an unconstrained quadratic optimization in \((A,b)\). Therefore, its optimal solution can be computed by taking the derivative of the objective, i.e., \(f(A,b) = \mathbb{E}_{x,y} \{ \Vert x - Ay - b \Vert^2 \}\) , w.r.t. \((A,b)\) and setting them to zero \[\begin{equation} \begin{split} 0 = \frac{\partial f}{\partial A} = 2 \mathbb{E}_{x,y} \{ (b + Ay -x) y^T \}, \\ 0 = \frac{\partial f}{\partial b} = 2 \mathbb{E}_{x,y} \{ b + Ay - x \}. \end{split} \tag{6.9} \end{equation}\] The second equation gives us the solution of \(b^\star\) \[\begin{equation} b^\star = \bar{x} - A \bar{y}. \tag{6.10} \end{equation}\] Plug the solution (6.10) back into the first equation in (6.9), we obtain \[\begin{equation} \mathbb{E}_{x,y} \{ (A(y - \bar{y}) - (x - \bar{x})) y^T\} = 0. \tag{6.11} \end{equation}\] On the other hand, we have \[\begin{equation} \left( \mathbb{E}_{x,y} \{ A (y - \bar{y}) - (x - \bar{x})\} \right) \bar{y}^T = 0. \tag{6.12} \end{equation}\] Subtracting (6.12) from (6.11), we have \[ \mathbb{E}_{x,y} \left\{ (A(y-\bar{y}) - (x - \bar{x})) (y - \bar{y})^T \right\} = 0, \] which is exactly \[ A \Sigma_{yy} - \Sigma_{xy} = 0. \] Therefore, we obtain the optimal \(A\) \[\begin{equation} A^\star = \Sigma_{xy} \Sigma^{-1}_{yy}. \tag{6.13} \end{equation}\] Combining (6.13) and (6.10), we get the optimal linear least-squares estimator \[ x^\star(y) = \Sigma_{xy} \Sigma^{-1}_{yy} y + \left( \bar{x} - \Sigma_{xy} \Sigma^{-1}_{yy} \bar{y} \right) = \bar{x} + \Sigma_{xy} \Sigma^{-1}_{yy} (y - \bar{y}). \] The error covariance (6.8) follows by direct computation.

We next list a few useful properties of the linear least-squares estimator.

Corollary 6.1 (Properties of the Linear Least-Squares Estimator) The linear least-squares estimator \(x^\star(y)\) in (6.7) is unbiased, i.e., \[ \mathbb{E}_y \{ x^\star(y) \} = \bar{x}. \]

The estimation error \(x - x^\star(y)\) is uncorrelated with both \(y\) and \(x^\star(y)\), i.e., \[\begin{equation} \begin{split} \mathbb{E}_{x,y} \{ (x - x^\star(y))y^T \} = 0. \\ \mathbb{E}_{x,y} \{ (x - x^\star(y)) (x^\star(y))^T \} = 0. \end{split} \tag{6.14} \end{equation}\]

Equation (6.14) is known as the orthogonal projection principle.

The next corollary considers the linear least-squares estimator of a new variable \(z\) that is a linear function of \(x\).

Corollary 6.2 Consider in addition to \(x\) and \(y\), the random vector \(z\) defined by \[ z = Cx, \] where \(C \in \mathbb{R}^{p \times n}\) is given. Then the linear least-squares estimator of \(z\) given \(y\) is \[ z^\star(y) = C x^\star(y), \] and the corresponding error covariance matrix is \[ \mathbb{E}_{z,y}\left\{ (z - z^\star(y))(z - z^\star(y))^T \right\} = C \mathbb{E}_{x,y} \left\{ (x - x^\star(y))(x - x^\star(y))^T \right\} C^T, \] where \(\mathbb{E}_{x,y} \left\{ (x - x^\star(y))(x - x^\star(y))^T \right\}\) is given in (6.8).

Proof. Since \(z = Cx\), we have \(\mathbb{E} \{ z \} = C \bar{x} = \bar{z}\), and \[ \Sigma_{zz} = \mathbb{E} \{ (z - \bar{z})(z - \bar{z})^T \} = C \Sigma_{xx} C^T, \\ \Sigma_{zy} = \mathbb{E} \{ (z - \bar{z})(y - \bar{y})^T \} = C \Sigma_{xy}, \\ \Sigma_{yz} = \mathbb{E} \{ (y - \bar{y}) (z - \bar{z})^T \} = \Sigma^T_{xy} C^T. \] The result then follows by applying Proposition 6.3 to \(z\) and \(y\).

The next corollary considers the linear least-squares estimator of \(x\) given \(z\), a random vector that is a linear function of \(y\).

Corollary 6.3 Consider in addition to \(x\) and \(y\), an additional random variable \(z\) \[ z = C y + u, \] where \(C \in \mathbb{R}^{p \times m}\), with rank \(p\), and \(u \in \mathbb{R}^p\) are given. Then the linear least-squares estimator of \(x\) given \(z\) is \[ x^\star(z) = \bar{x} + \Sigma_{xy} C^T (C \Sigma_{yy} C^T)^{-1} (z - C \bar{y} - u), \] and the corresponding error covariance matrix is \[ \mathbb{E}_{x,z}\left\{ (x - x^\star(z))(x - x^\star(z))^T \right\} = \Sigma_{xx} - \Sigma_{xy} C^T (C \Sigma_{yy} C^T)^{-1} C \Sigma_{xy}^T. \]

Proof. Since \(z = Cy + u\), we have \(\bar{z} = \mathbb{E}\{ z \} = C \bar{y} + u\), and \[ \Sigma_{zz} = \mathbb{E}\{ (z - \bar{z})(z - \bar{z})^T \} = C \Sigma_{yy} C^T, \\ \Sigma_{zx} = \mathbb{E}\{ (z - \bar{z})(x - \bar{x})^T \} = C \Sigma_{xy}^T, \\ \Sigma_{xz} = \mathbb{E}\{ (x - \bar{x})(z - \bar{z})^T \} = \Sigma_{xy}C^T. \] The result then follows by applying Proposition 6.3.

Frequently, we want to estimate a vector of parameters \(x \in \mathbb{R}^n\) given a measurement vector \(z \in \mathbb{R}^m\) of the form \(z = C x + v\) with \(C \in \mathbb{R}^{m \times n}\) a given matrix and \(v \in \mathbb{R}^m\) a noise vector. The following corollary gives the linear least squares estimator \(x^\star(z)\) and its error covariance.

Corollary 6.4 (Linear Least-Squares Estimator with Noise) Let \[ z = C x + v, \] where \(C \in \mathbb{R}^{m \times n}\) is a given matrix, and the random variable \(x\) and \(v\) are uncorrelated. Denote \[ \mathbb{E}\{x \} = \bar{x}, \quad \mathbb{E}\{ (x - \bar{x})(x - \bar{x})^T \} = \Sigma_{xx}, \\ \mathbb{E}\{ v\} = \bar{v}, \quad \mathbb{E}\{ (v - \bar{v})(v - \bar{v})^T \} = \Sigma_{vv}, \] and assume \(\Sigma_{vv}\) is positive definite. Then the linear least-squares estimator of \(x\) given \(z\) is \[ x^\star(z) = \bar{x} + \Sigma_{xx} C^T (C \Sigma_{xx} C^T + \Sigma_{vv})^{-1} (z - C \bar{x} - \bar{v}), \] and the corresponding error covariance is \[ \mathbb{E}_{x,v} \{ (x - x^\star(z))(x - x^\star(z))^T \} = \Sigma_{xx} - \Sigma_{xx}C^T (C \Sigma_{xx} C^T + \Sigma_{vv})^{-1} C \Sigma_{xx}. \]

Proof. Denote \[ y = \begin{bmatrix} x \\ v \end{bmatrix}, \quad \bar{y} = \begin{bmatrix} \bar{x} \\ \bar{v} \end{bmatrix}, \] then clearly we have \[ x = \underbrace{ \begin{bmatrix} I & 0 \end{bmatrix}}_{C_x} y, \] and \[ z = \underbrace{\begin{bmatrix} C & I \end{bmatrix}}_{\tilde{C}} y. \] Using Corollary 6.2, we have \[ x^\star(z) = C_x y^\star(z) \\ \mathbb{E}\{ (x - x^\star(z))(x - x^\star(z))^T \} = C_x \mathbb{E}\{(y - y^\star(z))(y - y^\star(z))^T \} C_x^T, \] where \(y^\star(z)\) is the linear least-sqaures estimator of \(y\) given \(z\).

To obtain \(y^\star(z)\), we can apply Corollary 6.3 with \(u=0\) and \(x=y\), leading to \[ y^\star(z) = \bar{y} + \Sigma_{yy} \tilde{C}^T (\tilde{C} \Sigma_{yy} \tilde{C}^T)^{-1} (z - \tilde{C}\bar{y}), \] and the error covariance \[ \mathbb{E}\{(y - y^\star(z))(y - y^\star(z))^T \} = \Sigma_{yy} - \Sigma_{yy} \tilde{C}^T (\tilde{C}\Sigma_{yy}\tilde{C}^T)^{-1} \tilde{C} \Sigma_{yy}. \] The result then follows by noting \[ \Sigma_{yy} = \begin{bmatrix} \Sigma_{xx} & 0 \\ 0 & \Sigma_{vv} \end{bmatrix} \] because \(x\) and \(v\) are uncorrelated.

The next two corollaries deal with least-squares estimators involving multiple measurements arriving sequentially. In particular, the corollaries show how to modify an existing least-squares estimate \(x^\star(y)\) to obtain \(x^\star(y,z)\) once an additional measurement \(z\) becomes available. This is a central operation in Kalman filtering.

Corollary 6.5 (Linear Least-Squares Estimator of Uncorrelated Measurements) Consider in addition to \(x\) and \(y\), an additional random vector \(z \in \mathbb{R}^p\) that is uncorrelated with \(y\). Then the linear least-squares estimator \(x^\star(y,z)\) of \(x\) given both \(y\) and \(z\) has the form \[ x^\star(y,z) = x^\star(y) + x^\star(z) - \bar{x}, \] where \(x^\star(y)\) and \(x^\star(z)\) are the linear least-squares estimates of \(x\) given \(y\) and given \(z\), respectively. Furthermore, the error covariance matrix is \[ \mathbb{E}_{x,y,z} \{ (x - x^\star(y,z))(x - x^\star(y,z))^T \} = \Sigma_{xx} - \Sigma_{xy} \Sigma^{-1}_{yy} \Sigma^T_{xy} - \Sigma_{xz} \Sigma^{-1}_{zz} \Sigma_{xz}^T, \] where \[ \Sigma_{xz} = \mathbb{E}_{x,z}\{ (x - \bar{x})(z - \bar{z})^T \}, \quad \Sigma_{zz} = \mathbb{E}_{z} \{ (z - \bar{z})(z - \bar{z})^T \}, \quad \bar{z} = \mathbb{E}_z \{ z \}, \] and it is assumed that \(\Sigma_{zz}\) and \(\Sigma_{yy}\) are both invertible.

Proof. Let \[ w = \begin{bmatrix} y \\ z \end{bmatrix}, \quad \bar{w} = \begin{bmatrix} \bar{y} \\ \bar{z} \end{bmatrix}. \] Then we can apply Proposition 6.3 to compute the linear least-squares estimator of \(x\) given \(w\) \[ x^\star(w) = \bar{x} + \Sigma_{xw} \Sigma^{-1}_{ww} (w - \bar{w}). \] On the other hand, we have \[ \Sigma_{xw} = \mathbb{E}\{ (x - \bar{x}) \begin{bmatrix} (y - \bar{y})^T & ( z - \bar{z} )^T \end{bmatrix} \} = \begin{bmatrix} \Sigma_{xy} & \Sigma_{xz} \end{bmatrix}, \] and since \(y\) and \(z\) are uncorrelated, we have \[ \Sigma_{ww} = \begin{bmatrix} \Sigma_{yy} & 0 \\ 0 & \Sigma_{zz} \end{bmatrix}. \] The result then follows by direct computation.

The next corollary generalizes the previous result to the case where \(y\) and \(z\) are correlated.

Corollary 6.6 (Linear Least-Squares Estimator of Correlated Measurements) Consider the situation in Corollary 6.5, but with \(z\) and \(y\) being correlated \[ \Sigma_{yz} = \mathbb{E}_{y,z} \{ (y - \bar{y})(z - \bar{z})^T \} \neq 0. \] Then \(x^\star(y,z)\) has the following form \[ x^\star(y,z) = x^\star(y) + x^\star(z - z^\star(y)) - \bar{x}, \] where \(x^\star(z - z^\star(y))\) denotes the linear least-squares estimate of \(x\) given the random vector \(z - z^\star(y)\) and \(z^\star(y)\) is the linear least-squares estimate of \(z\) given \(y\). Furthermore, the error covariance matrix is \[ \mathbb{E}_{x,y,z} \{ (x - x^\star(y,z))(x - x^\star(y,z))^T \} = \Sigma_{xx} - \Sigma_{xy} \Sigma^{-1}_{yy} \Sigma^T_{xy} - \hat{\Sigma}_{xz} \hat{\Sigma}^{-1}_{zz} \hat{\Sigma}^T_{xz}, \] where \[ \hat{\Sigma}_{xz} = \mathbb{E}_{x,y,z} \{ (x - \bar{x})(z - z^\star(y))^T \}, \quad \hat{\Sigma}_{zz} = \mathbb{E}_{y,z} \{ (z - z^\star(y))(z - z^\star(y))^T \}. \]

Proof. By Proposition 6.3, we know \(z^\star(y)\) is linear in \(y\) as \[ z^\star(y) = \bar{z} + \Sigma_{zy} \Sigma^{-1}_{yy} (y - \bar{y}) := B y + c, \] where \(B = \Sigma_{zy} \Sigma^{-1}_{yy}\) and \(c = \bar{z} - \Sigma_{zy} \Sigma^{-1}_{yy} \bar{y}\). The linear least-squares estimate of \(x\) given \((y,z)\) has the form \[\begin{equation} x = \begin{bmatrix} A_y^\star & A_z^\star \end{bmatrix} \begin{bmatrix} y \\ z \end{bmatrix} + b^\star, \tag{6.15} \end{equation}\] where \((A_y^\star, A_z^\star, b^\star)\) is solution to \[\begin{equation} (A_y^\star, A_z^\star, b^\star) = \arg\min_{A_y,A_z,b} \mathbb{E}_{x,y,z} \left\{ \Vert x - A_y y - A_z z - b \Vert^2 \right\}. \tag{6.16} \end{equation}\] The linear least-squares estimate of \(x\) given \((y, z - z^\star(y))\) has the form \[\begin{equation} x = \begin{bmatrix} G_y^\star & G_z^\star \end{bmatrix} \begin{bmatrix} y \\ z - By - c \end{bmatrix} + h^\star, \tag{6.17} \end{equation}\] where \((G_y^\star,G_z^\star,h^\star)\) is solution to \[\begin{equation} (G_y^\star,G_z^\star,h^\star) = \arg\min_{G_y,G_z,h} \mathbb{E}_{x,y,z} \left\{ \Vert x - G_y y - G_z (z - By - c) - h \Vert^2 \right\}. \tag{6.18} \end{equation}\] Observe that the objective in (6.18) can be rewritten as \[ \mathbb{E}_{x,y,z} \left\{ \Vert x - (G_y - G_z B) y - G_z z - (h - G_z c) \Vert^2 \right\}, \] when matched with the objective of (6.16) we have \[ A_y^\star = G_y^\star - G_z^\star B, \quad A_z^\star = G_z^\star, \quad b^\star = h^\star - G_z^\star c. \] As a result, the linear least-squares estimator in (6.17) becomes \[ x = (A_y^\star + A_z^\star B) y + A_z^\star (z - By - c) + b^\star + A_z^\star c = A^\star_y y + A^\star_z z + b^\star, \] which is the same as (6.15). Therefore, we have \[ x^\star(y,z) = x^\star(y, z - z^\star(y)). \]

From Corollary 6.1, we know \(y\) and \(z - z^\star(y)\) is uncorrelated. Consequently, we reduce to the uncorrelated setup in Corollary 6.5 and the result follows.

6.2 Kalman Filter

Consider now a linear dynamical system without control \[\begin{equation} \begin{cases} x_{k+1} = A_k x_k + w_k \\ y_k = C_k x_k + v_k \end{cases}, k=0,1,\dots,N-1, \tag{6.19} \end{equation}\] where \(x_k \in \mathbb{R}^n\) the state, \(w_k \in \mathbb{R}^n\) the random disturbance, \(y_k \in \mathbb{R}^d\) the measurement (output), and \(v_k \in \mathbb{R}^d\) the measurement noise.

We assume \(x_0,w_0,\dots,w_{N-1},v_0,\dots,v_{N-1}\) are independent random vectors with means \[ \mathbb{E}\{ w_k \} = \mathbb{E} \{ v_k \} = 0, \quad k=0,\dots,N-1, \] and covariances \[ \mathbb{E} \{ w_k w_k^T \} = M_k, \quad \mathbb{E} \{ v_k v_k^T \} = N_k, \quad k=0,\dots,N-1, \] with \(N_k\) positive definite for all \(k\). We assume the initial state \(x_0\) has mean \(\mathbb{E}\{ x_0 \}\) and covariance \[ S = \mathbb{E} \{ (x_0 - \mathbb{E}\{x_0 \} ) (x_0 - \mathbb{E}\{x_0 \} )^T \}. \] Let \[ Y_k = (y_0,\dots,y_k) \] be the set of measurements up to time \(k\), our goal is to obtain the linear least-squares estimate of \(x_k\) given \(Y_k\), denoted as \[ x^\star_{k \mid k} := x^\star_k (Y_k), \] and its error covariance matrix \[ \Sigma_{k \mid k} := \mathbb{E} \{ (x_k - x^\star_{k \mid k}) (x_k - x^\star_{k \mid k})^T\}. \] By definition, we have \[\begin{equation} x^\star_{0 \mid -1} = \mathbb{E}\{ x_0 \}, \quad \Sigma_{0 \mid -1} = S. \tag{6.20} \end{equation}\]

The Kalman filter (Rudolph Emil Kalman 1960) will derive a recursion to update \(x^\star_{k \mid k}\) and \(\Sigma_{k \mid k}\).

Road map. Towards this, let us assume we have computed \(x^\star_{k \mid k-1}\) and its error covariance \(\Sigma_{k \mid k-1}\) (the initial condition is given by (6.20)). Our goal is to compute \(x^\star_{k+1 \mid k}\) and its error covariance \(\Sigma_{k+1\mid k}\). We will see that, to compute \(x^\star_{k+1 \mid k}\), we compute \(x^\star_{k \mid k}\) first, and to compute \(\Sigma_{k+1 \mid k}\), we compute \(\Sigma_{k\mid k}\) first, as illustrated below. \[\begin{equation} \begin{split} \text{Update estimate:}\quad x^\star_{k \mid k-1} \longrightarrow x^\star_{k \mid k} \longrightarrow x^\star_{k+1 \mid k}. \\ \text{Update covariance:}\quad \Sigma_{k \mid k-1} \longrightarrow \Sigma_{k \mid k} \longrightarrow \Sigma_{k+1 \mid k}. \end{split} \end{equation}\]

Using the measurement. At time \(k\), we receive a new measurement \[ y_k = C_k x_k + v_k. \] We have \[ x^\star_{k\mid k} = x^\star_k (Y_k) = x^\star_k(Y_{k-1},y_k), \] by Corollary 6.6, we have \[\begin{equation} x^\star_{k \mid k} = x^\star_{k \mid k-1} + x^\star_k (y_k - y_k^\star(Y_{k-1})) - \mathbb{E}\{ x_k \}, \tag{6.21} \end{equation}\] where \(y_k^\star(Y_{k-1})\) is the linear least-squares estimate of \(y_k\) given \(Y_{k-1}\).

Simplify (6.21). First note that by Corollary 6.2 and independence of \(v_k\), we have \[ y_k^\star(Y_{k-1}) = C_k x^\star_{k \mid k-1}. \] We now need to compute \(x_k^\star(y_k - y_k^\star(Y_{k-1}))\). We do so by Proposition 6.3. The covariance matrix of \(y_k - y_k^\star(Y_{k-1})\) is, by Corollary 6.2, \[ \mathbb{E} \{ (y_k - y_k^\star(Y_{k-1}))(y_k - y_k^\star(Y_{k-1}))^T \} = C_k \Sigma_{k \mid k-1} C_k^T + N_k. \] The correlation between \(x_k\) and \(y_k - y_k^\star(Y_{k-1})\) is \[\begin{equation} \begin{split} \mathbb{E}\{ x_k (y_k - y_k^\star(Y_{k-1}))^T \} = \mathbb{E} \{ x_k(C_k (x_k - x^\star_{k\mid k-1}))^T \} + \underbrace{ \mathbb{E}\{ x_k v_k^T \} }_{=0 \text{ by independence of } v_k} \\ = \mathbb{E}\{(x_k - x^\star_{k \mid k-1}) (x_k - x^\star_{k \mid k-1})^T \}C_k^T + \underbrace{\mathbb{E}\{ x^\star_{k \mid k-1}(x_k - x^\star_{k \mid k-1})^T \}}_{=0 \text{ by the orthogonal projection principle}}C_k^T \\ = \Sigma_{k \mid k-1} C_k^T. \end{split} \end{equation}\] As a result, by Proposition 6.3, we have \[ x_k^\star(y_k - y_k^\star(Y_{k-1})) = \mathbb{E}\{x_k \} + \Sigma_{k \mid k-1} C_k^T (C_k \Sigma_{k \mid k-1} C_k^T + N_k)^{-1} (y_k - C_k x^\star_{k \mid k-1}). \]

Update the estimate. Thus, (6.21) is simplified as \[\begin{equation} x^\star_{k\mid k} = x^\star_{k \mid k-1} + \Sigma_{k \mid k-1} C_k^T (C_k \Sigma_{k \mid k-1} C_k^T + N_k)^{-1} (y_k - C_k x^\star_{k \mid k-1}), \tag{6.22} \end{equation}\] which describes the update from \(x^\star_{k \mid k-1}\) to \(x^\star_{k \mid k}\).

To update \(x^\star_{k+1 \mid k}\) from \(x^\star_{k \mid k}\), by Corollary 6.2, we have \[\begin{equation} x^\star_{k+1 \mid k} = A_k x^\star_{k \mid k}. \tag{6.23} \end{equation}\]

Update the covariance. The error covariance \(\Sigma_{k \mid k}\), by Corollary 6.6, can be written as \[\begin{equation} \Sigma_{k \mid k} = \Sigma_{k \mid k-1} - \Sigma_{k\mid k-1} C_k^T (C_k \Sigma_{k \mid k-1} C_k^T + N_k)^{-1} C_k \Sigma_{k \mid k-1}. \tag{6.24} \end{equation}\] (This requires just a little bit thinking.) To update \(\Sigma_{k+1 \mid k}\) from \(\Sigma_{k \mid k}\), we can use Corollary 6.2 and the independence of \(w_k\) to obtain \[\begin{equation} \Sigma_{k+1 \mid k} = A_k \Sigma_{k \mid k} A_k^T + M_k. \tag{6.25} \end{equation}\]

Equations (6.22)-(6.25) forms the Kalman Filter.

Including controls. When the dynamics includes control \[ x_{k+1} = A_k x_k + B_k u_k + w_k, \] the only change that needs to be made to the Kalman Filter is that (6.23) should be replaced by \[\begin{equation} x^\star_{k+1 \mid k} = A_k x^\star_{k \mid k} + B_k u_k. \tag{6.26} \end{equation}\]

6.2.1 Steady-State Kalman Filter

Combining the two updates on covariance matrices (6.24) and (6.25), we obtain \[\begin{equation} \Sigma_{k+1 \mid k} = A_k (\Sigma_{k \mid k-1} - \Sigma_{k \mid k-1} C_k^T (C_k \Sigma_{k \mid k-1} C_k^T + N_k)^{-1} C_k \Sigma_{k \mid k-1} ) A_k^T + M_k, \tag{6.27} \end{equation}\] which is the same as the discrete-time Riccati equation (2.7) when we study the solution of the finite-horizon LQR problem in Proposition 2.1.

When \(A_k, C_k, M_k, N_k\) are constant matrices \[ A_k = A, \quad C_k = C, \quad, M_k = M, \quad N_k = N, \] the recursion (6.27) tends to the algebraic Riccati equation \[\begin{equation} \Sigma = A(\Sigma - \Sigma C^T(C \Sigma C^T + N)^{-1}C \Sigma)A^T + M, \tag{6.28} \end{equation}\] for which a unique positive definite solution \(\Sigma\) exists if \((A,C)\) is observable and \((A,D)\) is controllable with \(M = D D^T\). Then, using equation (6.24), we have that \(\Sigma_{k \mid k}\) tends to \[ \bar{\Sigma} = \Sigma - \Sigma C^T (C \Sigma C^T + N)^{-1} C \Sigma. \] This leads to the simple steady-state Kalman filter \[\begin{equation} x^\star_{k \mid k} = \underbrace{A x^\star_{k-1 \mid k-1}}_{\text{prediction}} + \underbrace{\Sigma C^T(C \Sigma C^T + N)^{-1} (y_k - CA x_{k-1 \mid k-1})}_{\text{feedback correction}}. \tag{6.29} \end{equation}\]

6.2.2 Continuous-time Kalman Filter

Consider the continuous-time analog of the linear system in (6.19) \[\begin{equation} \begin{cases} \dot{x} = A x + Bu + w \\ y = C x + v \end{cases} \tag{6.30} \end{equation}\] where \(x \in \mathbb{R}^n\) the state, \(u \in \mathbb{R}^m\) the control, \(y \in \mathbb{R}^d\) the measurement, and \(w,v\) are white noises with \[ \mathbb{E}\{w\}=0, \quad \mathbb{E}\{ w w^T \} = M, \quad \mathbb{E}\{v\} = 0, \quad \mathbb{E}\{ v v^T\} = N. \]

Suppose the initial state \(x(0)\) satisfies \[ \mathbb{E}\{ x(0) \} = \hat{x}_0, \quad \mathbb{E}\{ (x(0) - \hat{x}_0) (x(0) - \hat{x}_0)^T \} = \Sigma_0. \] Then the continuous-time Kalman Filter updates the state estimate as \[\begin{equation} \dot{\hat{x}} = \underbrace{A \hat{x} + Bu}_{\text{prediction}} + \underbrace{K (y - C \hat{x})}_{\text{feedback correction}}, \tag{6.31} \end{equation}\] where \(K\) is a feedback gain computed by \[ K = \Sigma C^T N^{-1}, \] with \(\Sigma\) satisfying the following differential equation \[\begin{equation} \dot{\Sigma} = A \Sigma + \Sigma A^T + M - \Sigma C^T N^{-1} C \Sigma. \tag{6.32} \end{equation}\] Similarly, at steady state, the differential equation (6.32) tends to the continuous-time algebraic Riccati equation \[ 0 = A \Sigma + \Sigma A^T + M - \Sigma C^T N^{-1} C \Sigma. \]

6.3 Linear Quadratic Gaussian Control

With our knowledge about the Kalman filter, we are ready to solve a particular instance of output-feedback control, known as the Linear Quadratic Gaussian (LQG) control.

Consider the discrete-time linear dynamical system: \[\begin{equation} \begin{cases} x_{k+1} = A_k x_k + B_k u_k + w_k \\ y_k = C_k x_k + v_k \end{cases}, \quad k=0,\dots,N-1, \tag{6.33} \end{equation}\] where \(w_k\) and \(v_k\) are white noises with \[ \mathbb{E}\{ w_k \} = 0, \mathbb{E}\{ v_k \} = 0, \quad k=0,\dots,N-1, \\ \mathbb{E} \{ w_k w_k^T \} = M_k, \mathbb{E} \{ v_k v_k^T \} = N_k, \quad k=0,\dots,N-1. \] Assume the initial state \(x_0\) follows a Gaussian distribution \(x_0 \sim \mathcal{N}(\bar{x}_0, S)\). This is the same setup as Section 6.2 Kalman filter.

The goal of the LQG control is \[\begin{equation} \min_{u_k,k=0,\dots,N-1} \mathbb{E} \left\{ x_N^T Q_N x_N + \sum_{k=0}^{N-1} (x_k^T Q_k x_k + u_k^T R_k u_k) \right\}, \tag{6.34} \end{equation}\] where the expectation is taken over the randomness of both \(w_k\) and \(v_k\). The LQG cost function (6.34) reads exactly the same as the LQR problem in (2.2). However, the key difference between the LQG problem (6.34) and the LQR problem (2.2) is that in LQR the controller has full access to the state \(x_k\) of the system, while in LQG the controller only has access to a sequence of measurements \[ Y_k = \{y_0,\dots,y_k \}. \]

We will now show that the Kalman filter brings us back to the setup of LQR.

Let us rewrite the cost \[ \mathbb{E}\{x_k^T Q_k x_k \} = \mathbb{E} \left\{ \mathbb{E} \{ x_k^T Q_k x_k \mid Y_k \} \right\} = \mathbb{E} \left\{ \mathbb{E} \{ (x_k - x^\star_{k \mid k} + x^\star_{k \mid k})^T Q_k (x_k - x^\star_{k \mid k} + x^\star_{k \mid k}) \mid Y_k \} \right\} \\ = \mathbb{E}\left\{ \mathbb{E}\{ (x_k - x^\star_{k \mid k})^T Q_k (x_k - x^\star_{k \mid k}) + 2 (x^\star_{k \mid k})^T Q_k (x_k - x^\star_{k \mid k}) + (x^\star_{k \mid k})^T Q_k x^\star_{k \mid k} \mid Y_k\} \right\} \\ = \mathbb{E}\{ (x^\star_{k \mid k})^T Q_k x^\star_{k \mid k} \} + \underbrace{\mathbb{E}\{ \mathbb{E}\{ 2 (x^\star_{k \mid k})^T Q_k (x_k - x^\star_{k \mid k}) \mid Y_k \} \}}_{=0 \text{ due to orthogonal projection principle}} + \underbrace{\mathbb{E}\{ (x_k - x^\star_{k \mid k})^T Q_k (x_k - x^\star_{k \mid k}) \}}_{=\text{tr}(Q_k \Sigma_{k \mid k})}, \] where \(x^\star_{k\mid k}\) is the Kalman filter estimate of the state (i.e., the linear least squares estimate, or the conditional expectation). Note that from the Kalman filter we know the error covariance \(\Sigma_{k \mid k}\) (and hence \(\text{tr}(Q_k \Sigma_{k \mid k})\)) is independent from the control. Therefore, the LQG problem (6.34) is equivalent to the following LQR problem \[\begin{equation} \min_{u_k, k=0,\dots,N-1} \mathbb{E} \left\{ (x^\star_{N\mid N})^T Q_N x^\star_{N\mid N} + \sum_{k=0}^{N-1} (x^\star_{k \mid k})^T Q_k x^\star_{k \mid k} + u_k^T R_k u_k \right\}, \tag{6.35} \end{equation}\] for which we know the optimal control is (according to Proposition 2.1) \[\begin{equation} u_k^\star = - \underbrace{(R_k + B_k^T S_{k+1} B_k)^{-1} B_k^T S_{k+1} A_k}_{K_k} x^\star_{k \mid k}, \tag{6.36} \end{equation}\] with \(S_k\) computed backwards as \(S_N = Q_N\), \[\begin{equation} S_k = Q_k + A_k^T \left[ S_{k+1} - S_{k+1} B_k (R_k + B_k^T S_{k+1} B_k)^{-1} B_k^T S_{k+1} \right] A_k. \tag{6.37} \end{equation}\]

In summary, to implement the optimal controller for LQR problem, we need to

• Compute \(S_k\) backwards in time according to (6.37)

• Run the Kalman filter (6.22) and (6.23) to obtain \(x^\star_{k \mid k}\)

• Compute control according to (6.36)

Separation theorem. Our derivation above shows that the optimal output-feedback control for LQG consists of (i) an optimal estimator, the Kalman filter, and (ii) an optimal state-feedback controller, the LQR controller.

6.3.1 Steady-state LQG

In steady-state LQG, we consider the dynamical system \[\begin{equation} \begin{cases} x_{k+1} = A x_k + B u_k + w_k \\ y_k = C x_k + v_k \end{cases}, \quad k=0,\dots \end{equation}\] where \(\mathbb{E}\{ w_k\} =0, \mathbb{E}\{ v_k\} = 0\), and \[ \mathbb{E}\{w_k w_k^T \} = M, \quad \mathbb{E}\{v_k v_k^T \} = N. \] The LQG control problem is \[\begin{equation} \min \mathbb{E} \left\{ \sum_{k=0}^{\infty} (x_k^T Q_k x_k + u_k^T R_k u_k) \right\}. \end{equation}\] The optimal controller is \[ u^\star_k = - \left[ (R + B^T S B)^{-1} B^T S A \right]x^\star_{k \mid k}, \] where \(S\) is the solution to the discrete-time algebraic Riccati equation \[ S = Q + A^T \left[ S - SB (R + B^T S B)^{-1} B^T S \right]A, \] and \(x^\star_{k\mid k}\) comes from the steady-state Kalman filter \[ x_{k \mid k}^\star = A x^\star_{k-1\mid k-1} + B u_{k-1} + \Sigma C^T (C \Sigma C^T + N)^{-1} (y_k - C(A x^\star_{k-1\mid k-1} + B u_{k-1})), \] with \(\Sigma\) the solution to another discrete-time algebraic Riccati equation \[ \Sigma = M + A\left[ \Sigma - \Sigma C^T (N + C \Sigma C^T)^{-1} C \Sigma \right]A^T. \]

Example 6.1 (LQG Stabilization of Simple Pendulum) Consider the pendulm dynamics that has already been shifted such that \(x=[\theta,\dot{\theta}]=0\) represents the upright position that we want to stabilize (cf. Example 2.1) \[ \dot{x} = \begin{bmatrix} x_2 \\ \frac{1}{ml^2} (u - b x_2 + mgl \sin x_1) \end{bmatrix} + \begin{bmatrix} 0 \\ w \end{bmatrix}, \] where \(w\) is a random white noise.

Linearizing the dynamics around \(x=0\) we have \[ \dot{x} \approx \underbrace{\begin{bmatrix} 0 & 1 \\ \frac{g}{l} & - \frac{b}{ml^2} \end{bmatrix}}_{A_c} x + \underbrace{\begin{bmatrix} 0 \\ \frac{1}{ml^2} \end{bmatrix}}_{B_c} u + \begin{bmatrix} 0 \\ w \end{bmatrix}. \]

We convert the continuous-time dynamics to discrete time with a fixed discretization \(h\) \[ x_{k+1} = \dot{x}_k \cdot h + x_k = (h \cdot A_c + I) x_k + (h\cdot B_c) u_k + h \begin{bmatrix} 0 \\ w \end{bmatrix} \\ = A x_k + B u_k + w_k. \]

We assume we can only observe the angular position of the pendulum \[ y_k = \underbrace{\begin{bmatrix} 1 & 0 \end{bmatrix}}_{C} x_k + v_k, \] with \(v_k\) some white noise.

We start with the true initial state \(x_0 = [2;-2]\), but with a noisy estimate \(x^\star_{0 \mid 0} = [0;0]\). Implementing the steady-state LQG controller produces the following result.

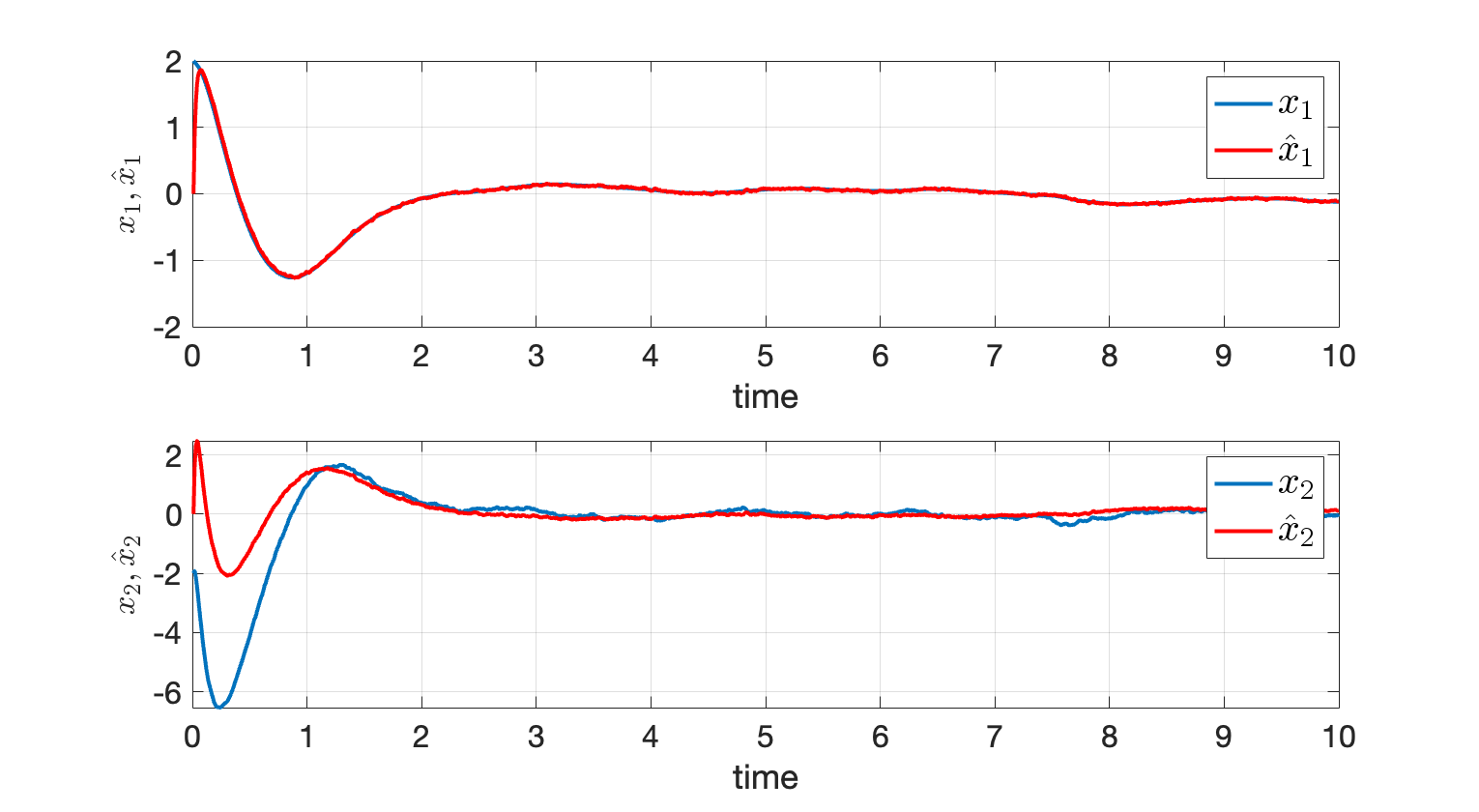
Figure 6.1: LQG Stabilization of Simple Pendulum.

You can find code for this example here.

Closed-loop analysis. Now that we have the Kalman filter and LQR controller implemented, let us take a look at the closed-loop response of the system. To ease our notation, let us denote \(\hat{x}_k := x^\star_{k \mid k}\) as the Kalman estimate of state. Then we can write the LQG controller as \[\begin{equation} \begin{cases} \hat{x}_{k+1} = A \hat{x}_k + B u_k + L (y_{k+1} - C(A \hat{x}_k + B u_k) ) & \text{Kalman filter}\\ x_{k+1} = A x_k + B u_k + w_k & \text{Original dynamics} \end{cases}, \tag{6.38} \end{equation}\] where \(L\) is the Kalman gain. The first equation can be simplified as \[ \hat{x}_{k+1} = A \hat{x}_k + Bu_k + L( C\underbrace{(A x_k + B u_k + w_k)}_{x_{k+1}} + v_{k+1} - CA\hat{x}_k - CB u_k )\\ = A \hat{x}_k + Bu_k + L (CA x_k - CA \hat{x}_k + C w_k + v_{k+1}) \] Let us denote the estimation error as \(e_k = x_k - \hat{x}_k\), the above equation becomes \[ \hat{x}_{k+1} = A \hat{x}_k + B u_k + LCA e_k + LC w_k + L v_{k+1} \] Subtracting the equation above from the second equation of (6.38), we have \[\begin{equation} e_{k+1} = (A - LCA) e_k + (I - LC) w_k - L v_{k+1}, \tag{6.39} \end{equation}\] which describes the evolution of the error dynamics. Now with \[ u_k = - K \hat{x}_k = -K (x_k - e_k) = K e_k - K x_k \] inserted into the second equation of (6.38), we have \[\begin{equation} x_{k+1} = (A - BK) x_k + BK e_k + w_k, \tag{6.40} \end{equation}\] which describes the evolution of the true state dynamics. Combining (6.39) and (6.40), we have the closed-loop system \[\begin{equation} \begin{bmatrix} x_{k+1} \\ e_{k+1} \end{bmatrix} = \underbrace{\begin{bmatrix} A - BK & BK \\ 0 & A - LCA \end{bmatrix}}_{A_{\mathrm{cl}}} \begin{bmatrix} x_k \\ e_k \end{bmatrix} + \begin{bmatrix} w_k \\ (I - LC) w_k - L v_{k+1} \end{bmatrix}. \tag{6.41} \end{equation}\] Now observe that if the Kalman gain \(L\) is stable, then \(e_{k}\) tends to zero with some noise. In this case, if the LQR gain \(K\) is stable, then the state \(x_k\) also tends to zero with some noise. In fact, since \(A_{\mathrm{cl}}\) is block-diagonal, we know the eigenvalues of \(A_{\mathrm{cl}}\) contains those of \(A - BK\) and those of \(A - LC A\).

6.3.2 Continuous-time LQG

6.4 Nonlinear Filtering

Kalman filter is the optimal filter for linear dynamics, linear measurements, and Gaussian noises. However, interesting real-world systems are often nonlinear \[\begin{equation} \begin{cases} x_{k+1} = f(x_k) + w_k, \\ y_k = h(x_k) + v_k \end{cases}, \tag{6.42} \end{equation}\] where \(w_k\) is white disturbance \(\mathbb{E}\{ w_k\} =0, \mathbb{E}\{ w_k w_k^T\} = M_k\), \(v_k\) is white measurement noise \(\mathbb{E}\{ v_k\} = 0, \mathbb{E} \{v_k v_k^T \} = N_k\), and \(f,g\) are assumed to be differentiable nonlinear functions.

A nonlinear filter follows the general strategy of a Kalman filter \[\begin{equation} \begin{split} \text{Update estimate:}\quad \hat{x}_{k \mid k-1} \overset{(3)}{\longrightarrow} \hat{x}_{k \mid k} \overset{(1)}{\longrightarrow} \hat{x}_{k+1 \mid k}. \\ \text{Update covariance:}\quad \Sigma_{k \mid k-1} \overset{(4)}{\longrightarrow} \Sigma_{k \mid k} \overset{(2)}{\longrightarrow} \Sigma_{k+1 \mid k}. \end{split} \end{equation}\] where I have replaced \(x^\star\) with \(\hat{x}\) because the estimator is often not optimal in the case of nonlinear functions.

6.4.1 Extended Kalman Filter

The key idea of extended Kalman filter (EKF) is to linearize the nonlinear functions \(f\) and \(h\).

Prediction (1) and (2). To perform prediction update according to the dynamics, we linearize \(f\) around \(\hat{x}_{k\mid k}\) \[ x_{k+1} = f(x_k) + w_k = f(\hat{x}_{k\mid k}) + J_f(\hat{x}_{k \mid k})(x_k - \hat{x}_{k \mid k}) + w_k + \text{h.o.t.}, \] where \(\text{h.o.t.}\) standards for high-order terms, and \(J_f\) is the Jacobian of the vector function \(f\): \[ J_f = \begin{bmatrix} \frac{\partial f_1}{x_1} & \cdots & \frac{\partial f_1}{\partial x_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial f_n}{\partial x_1} & \cdots & \frac{\partial f_n}{\partial x_n} \end{bmatrix}. \] With this linearization, update (1) of EKF is simply \[\begin{equation} \hat{x}_{k+1 \mid k} = f(\hat{x}_{k \mid k}), \tag{6.43} \end{equation}\] and covariance update (2) is \[\begin{equation} \Sigma_{k+1\mid k} = M_k + J_f(\hat{x}_{k \mid k}) \Sigma_{k \mid k} J_f^T (\hat{x}_{k \mid k}). \tag{6.44} \end{equation}\]

Correction (3) and (4). To perform measurement correction from \(y_k\), we linearize \(h\) around \(\hat{x}_{k \mid k-1}\) \[ y_{k} = h(x_k) + v_k = h(\hat{x}_{k \mid k-1}) + J_h(\hat{x}_{k \mid k-1}) (x_k - \hat{x}_{k \mid k-1}) + v_k + \text{h.o.t.}. \] With this linearization, update (3) of EKF is \[\begin{equation} \hspace{-10mm} \hat{x}_{k \mid k} = \hat{x}_{k \mid k-1} + \Sigma_{k\mid k-1}J_h^T(\hat{x}_{k\mid k-1}) ( J_h(\hat{x}_{k\mid k-1})\Sigma_{k \mid k-1} J_h^T(\hat{x}_{k\mid k-1}) + N_k )^{-1}(y_k - h(\hat{x}_{k\mid k-1})), \tag{6.45} \end{equation}\] and update (4) of EKF is \[\begin{equation} \hspace{-10mm}\Sigma_{k \mid k-1} - \Sigma_{k \mid k-1} \Sigma_{k\mid k-1}J_h^T(\hat{x}_{k\mid k-1}) ( J_h(\hat{x}_{k\mid k-1})\Sigma_{k \mid k-1} J_h^T(\hat{x}_{k\mid k-1}) + N_k )^{-1} J_h(\hat{x}_{k \mid k-1}) \Sigma_{k \mid k-1}. \tag{6.46} \end{equation}\]

Compared with the original Kalman filter in (6.22)-(6.25), we can see that EKF (6.43)-(6.46) (i) replaces \(A_k\) with the Jacobian \(J_f(\hat{x}_{k \mid k})\), (ii) replaces \(C_k\) with the Jacobian \(J_h(\hat{x}_{k \mid k-1})\), and (iii) replaces \(C_k \hat{x}_{k \mid k-1}\) with \(h(\hat{x}_{k \mid k-1})\) (those are the expected measurements).

When does EKF perform well? Since EKF is based on linearization, it performs well when (i) the functions \(f,g\) are locally linear around the linearization points, and (ii) there is less uncertainty in the covariance matrices \(\Sigma_{k \mid k-1},\Sigma_{k \mid k}\). Good illustrations can be found in Fig. 3.5 and Fig. 3.6 of (Thrun, Burgard, and Fox 2005).

Guarantees. Under the technical conditions in (Reif et al. 1999), the estimation error of EKF can be guaranteed to be bounded.

6.4.2 Unscented Kalman Filter

In nonlinear filtering, usually the distribution of the true state is never a Gaussian distribution. The key idea of unscented Kalman filter is to use a set of so-called “Sigma points” to capture the most important statistical properties of the true distribution, notably the first and second-order moments (i.e., mean and covariance).

Sigma points. Given a distribution with mean and covariance \((\mu, \Sigma)\) (assume the random variable has dimension \(n\)), it can be shown that \((2n+1)\) Sigma points can be chosen to match the mean and covariance (Van Der Merwe 2004) \[\begin{equation} \begin{split} x^0 = \mu, \\ x^i = \mu + \left[\sqrt{(n+\lambda)\Sigma} \right]_{i}, \quad i = 1,\dots,n, \\ x^{i} = \mu - \left[\sqrt{(n+\lambda)\Sigma} \right]_{i-n}, \quad i=n+1,\dots,2n, \end{split} \end{equation}\] where \(\sqrt{(n+\lambda)\Sigma}\) denotes the square root of the matrix \((n+\lambda)\Sigma\), \([\cdot]_i\) denotes the \(i\)-th column of the matrix, and \[ \lambda = \alpha^2(n+\kappa) - n, \] is a scaling parameter determined by hyperparameters \(\alpha\) and \(\kappa\) (\(\alpha\) usually set between \(10^{-2}\) and \(1\), and \(\kappa\) is usually set to either \(0\) or \(3-n\)). Each of the Sigma point also comes with two weights as \[ w^0_m = \frac{\lambda}{n+\lambda}, w^0_c = \frac{\lambda}{n+\lambda} + (1 - \alpha^2 + \beta), \\ w^i_m = w^i_c = \frac{1}{2(L + \lambda)}, \quad i=1,\dots,2n, \] where \(\beta\) is an extra hyperparameter (for Gaussian \(\beta=2\)).

Now we are ready to use the idea of Sigma points to present the unscented Kalman filter (UKF).

Prediction (1) and (2). To perform the prediction step, we generate \(2n+1\) Sigma points from the distribution \((\hat{x}_{k \mid k}, \Sigma_{k \mid k})\): \[ \bar{x}^0_{k \mid k}, \dots, \bar{x}^{2n}_{k \mid k}. \] The estimate \(\hat{x}_{k+1\mid k}\) is updated as the sample mean of evaluating \(f\) on all Sigma points \[\begin{equation} \hat{x}_{k+1 \mid k} = \sum_{i=0}^{2n} w^i_m f(\bar{x}^{i}_{k \mid k}), \tag{6.47} \end{equation}\] and the covariance estimate is updated as the sample covariance \[\begin{equation} \Sigma_{k+1 \mid k} = M_k + \sum_{i=0}^{2n} w^i_c (f(\bar{x}^{i}_{k \mid k}) - \hat{x}_{k+1 \mid k})(f(\bar{x}^{i}_{k \mid k}) - \hat{x}_{k+1 \mid k})^T, \tag{6.48} \end{equation}\] where \(M_k\) comes from the disturbance \(w_k\) in the dynamics.

Correction (3) and (4). To understand the UKF measurement correction, we need to present a key observation of the original Kalman filter. In (6.22) and (6.24), the matrix \[ C_k \Sigma_{k \mid k-1} C_k^T + N_k \] can be interpreted as the covariance of the measurement \(y_k\) (conditioned on all past measurements), i.e., \(\Sigma_{yy,k}\), due to the measurement function \(y_k = C_k x_k + v_k\), while the matrix \[ \Sigma_{k \mid k-1} C_k^T \] can be interpreted as the correlation between \(x_k\) and \(y_k\), i.e., \(\Sigma_{xy,k}\).

Now that we have Sigma points in UKF, we can use them to approximate \(\Sigma_{yy,k}\) and \(\Sigma_{xy,k}\). To do so, we first generate \((2n+1)\) Sigma points from the distribution \((\hat{x}_{k \mid k-1}, \Sigma_{k \mid k-1})\) \[ \bar{x}^0_{k \mid k-1}, \dots, \bar{x}^{2n}_{k \mid k-1}. \] We then compute the expected measurements of these Sigma points \[ \bar{y}^i_{k \mid k-1} = h(\bar{x}^i_{k \mid k-1}), i=0,\dots,2n. \] The sample mean of these measurements is \[ \hat{y}_{k \mid k-1} = \sum_{i=0}^{2n} w^i_m \bar{y}^i_{k \mid k-1}, \] and the sample covariance is \[ \Sigma_{yy,k} = N_k + \sum_{i=0}^{2n} w^i_c (\bar{y}^i_{k \mid k-1} - \hat{y}_{k \mid k-1})(\bar{y}^i_{k \mid k-1} - \hat{y}_{k \mid k-1})^T. \] The sample correlation between \(x\) and \(y\) can be computed as \[ \Sigma_{xy,k} = \sum_{i=0}^{2n} w^i_c (\bar{x}^i_{k \mid k-1} - \hat{x}_{k \mid k-1}) (\bar{y}^i_{k \mid k-1} - \hat{y}_{k \mid k-1})^T. \] As a result, the Kalman gain matrix is \[ L_k = \Sigma_{xy,k} \Sigma^{-1}_{yy,k}. \] The UKF update (3) is therefore \[\begin{equation} \hat{x}_{k \mid k} = \hat{x}_{k \mid k-1} + L_k (y_k - \hat{y}_{k \mid k-1}), \tag{6.49} \end{equation}\] and the update (4) is \[\begin{equation} \Sigma_{k \mid k} = \Sigma_{k \mid k-1} - L_k \Sigma_{yy,k} L_k^T. \tag{6.50} \end{equation}\]

Applications of EKF and UKF. Perhaps one of the most of well-known applications of EKF and UKF is simultaneous location and mapping (SLAM) in mobile robotics. Matlab has a nice demo that I recommend you to play with.

6.4.3 Particle Filter

Kalman filter, EKF, and UKF all represent the uncertainty of the state as Gaussian distributions, specifically as means and covariances. However, as mentioned before, the true distribution of the state is rarely a Gaussian distribution. How can we faithfully represent non-Gaussian distributions?

The UKF does provide us with a possible solution. UKF represents the Gaussian distribution by \(2n+1\) Sigma points. What if we generalize this idea by allowing more points, or in other words, represent a distribution by random samples?

This is the basic idea of a particle filter, which is arguably one of the most high-impact nonlinear filtering techniques. The idea of a particle filter is simple to state. Consider the dynamical system (6.42), but this time assume we know the distribution of \(w_k\) and \(v_k\). For example, in the case of a Gaussian distribution \(\mathcal{N}(\mu,\Sigma)\) (with dimension \(n\)), we know its probability density function is \[\begin{equation} \mathbb{P}(x = \xi) = \frac{\exp\left( -\frac{1}{2} (\xi- \mu)^T \Sigma^{-1} (\xi - \mu) \right)}{\sqrt{(2\pi)^n \det \Sigma}}. \tag{6.51} \end{equation}\] The goal of a nonlinear filter is to estimate the conditional distribution (or sometimes called the belief) of \(x_k\) given all previous measurements \(Y_k = (y_0,\dots,y_k)\) \[ p(x_k \mid Y_k). \] Since the conditional distribution generally cannot be written analytically, a particle filter will represent the conditional distribution as a set of samples, i.e., \[ \mathcal{X}_{k\mid k} = \{x_{k \mid k}^1,\dots,x_{k\mid k}^M \} \sim p(x_k \mid Y_k), \] where \(M\) is the total number of samples. The particle filter will then update the set of samples, using a similar prediction-correction two-step approach: \[ \mathcal{X}_{k \mid k} \overset{\text{prediction}}{\longrightarrow} \mathcal{X}_{k+1 \mid k} \overset{\text{correction}}{\longrightarrow} \mathcal{X}_{k+1 \mid k+1}, \] where the prediction step leverages the dynamics, and the correction step leverages the measurement function.

Prediction. The prediction step is straightforward \[ \mathcal{X}_{k+1\mid k} = \{x^i_{k+1\mid k} \}_{i=1}^M, \quad x_{k+1\mid k}^i = f(x^i_{k\mid k}) + w_k^i, i=1,\dots,M, \] which basically passes each sample in \(\mathcal{X}_{k\mid k}\) through the nonlinear dynamics \(f\) and then add a random disturbance. Note that \(w_k^i\) follows the known distribution of the noise that we know how to sample from, for example it can be the Gaussian distribution in (6.51).

Correction. The correction step will leverage the new measurement, \(y_{k+1}\), to adjust the set of samples. Particularly, we will evaluate the probability of observing \(y_{k+1}\) for each of the samples in the set \(\mathcal{X}_{k+1 \mid k}\), that is \[ \alpha_{k+1}^i = p(y_{k+1} \mid x_{k+1\mid k}^i), i=1,\dots,M. \] This is simply the probability of \[ \alpha_{k+1}^i = \mathbb{P}(v_{k+1} = y_{k+1} - h(x_{k+1\mid k}^i)), \] which can be computed since we know the distribution of \(v_{k+1}\). For example, if the distribution of \(v_{k+1}\) is Gaussian, then we can evaluate the probability using (6.51). Intuitively, the higher \(\alpha_{k+1}^i\) is, the more likely it is for the true state to be \(x_{k+1\mid k}^i\). Therefore, effectively, we have obtained a set of samples together with their probabilities \[ \{ (x_{k+1\mid k}^i, \alpha_{k+1}^i) \}_{i=1}^M. \] The next step is to perform importance sampling. In particular, we will generate a new set of \(M\) samples by sampling (with replacement) from the population \(\mathcal{X}_{k+1 \mid k}\) with the probability of sampling the \(i\)-th sample being \(\alpha_{k+1}^i\). This leads to the new sample set \(\mathcal{X}_{k+1 \mid k+1}\).

Hopefully you see that the particle filter is very easy to implement. Let us work on a simple example.

Example 6.2 (Robot Localization by Nonlinear Filtering) Consider a 2D robot with state \(s = (x,y,\theta)\) where \((x,y)\) is the position and \(\theta\) is the heading. The robot has two controls, the first one being the linear velocity \(l\), and the second one being the angular velocity (steering) \(u\). Therefore, the dynamics of the robot is \[ \begin{bmatrix} x_{k+1} \\ y_{k+1} \\ \theta_{k+1} \end{bmatrix} = \begin{bmatrix} x_k + (l \cos \theta_k)\Delta t \\ y_k + (l \sin \theta_k)\Delta t \\ \theta_k + u \Delta t \end{bmatrix} + w_k, \] where \(w_k\) is assumed to be some Gaussian noise, and \(\Delta t\) is time discretization.

There are a set of \(N\) landmarks in the environment, each with location \[ (x_{lm,i},y_{lm,i}),i=1,\dots,N. \] The robot is equipped with a sensor that measures distance from each landmark \[ o_k = \begin{bmatrix} \vdots \\ o_{k,i} \\ \vdots \end{bmatrix} + v_k, \quad o_{k,i} = \sqrt{(x_k - x_{lm,i})^2 + (y_k - y_{lm,i})^2}, i=1,\dots,N, \] where \(v_k\) is assumed to be known Gaussian noise.

We can implement a particle filter for localizing the robot given distance measurements from the landmarks.

We set \(N=20\) landmarks, in the beginning, the prior estimation of the robot location is completely wrong, as shown in Fig. 6.2.

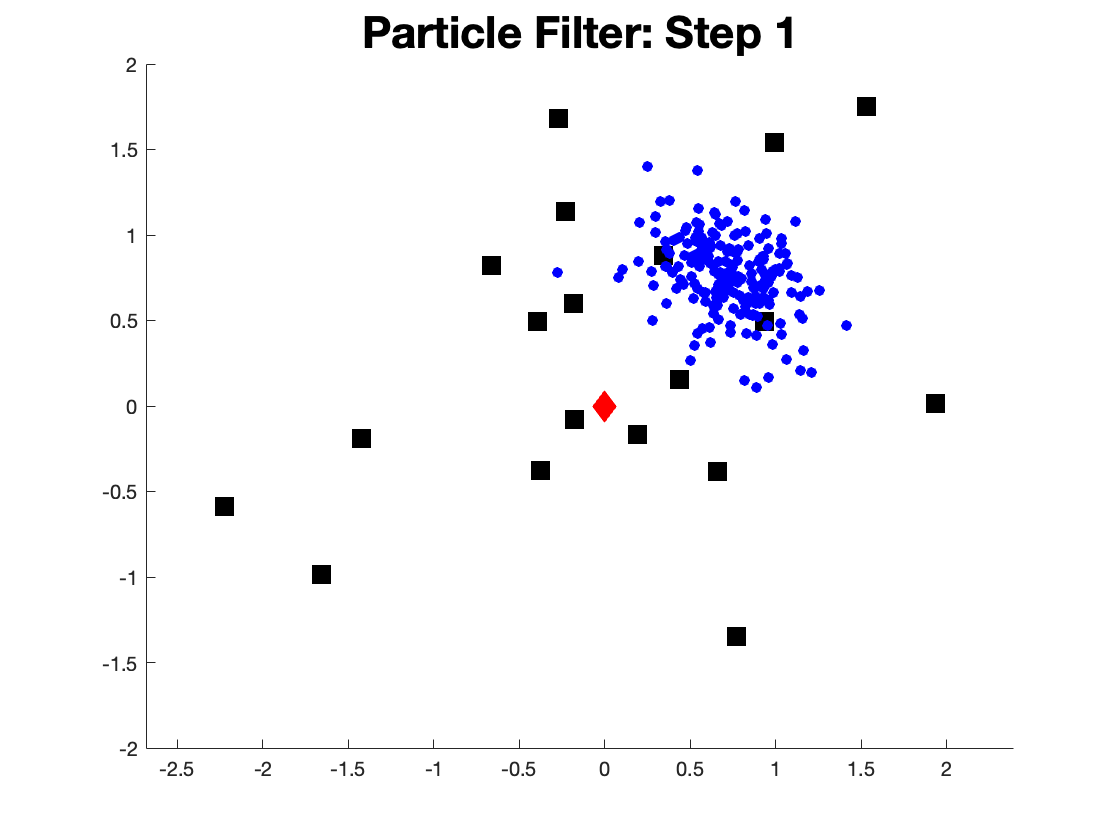
Figure 6.2: Initial estimate of the robot location.

After 200 steps of particle filter, we can see the particles cluster around the groundtruth robot location.

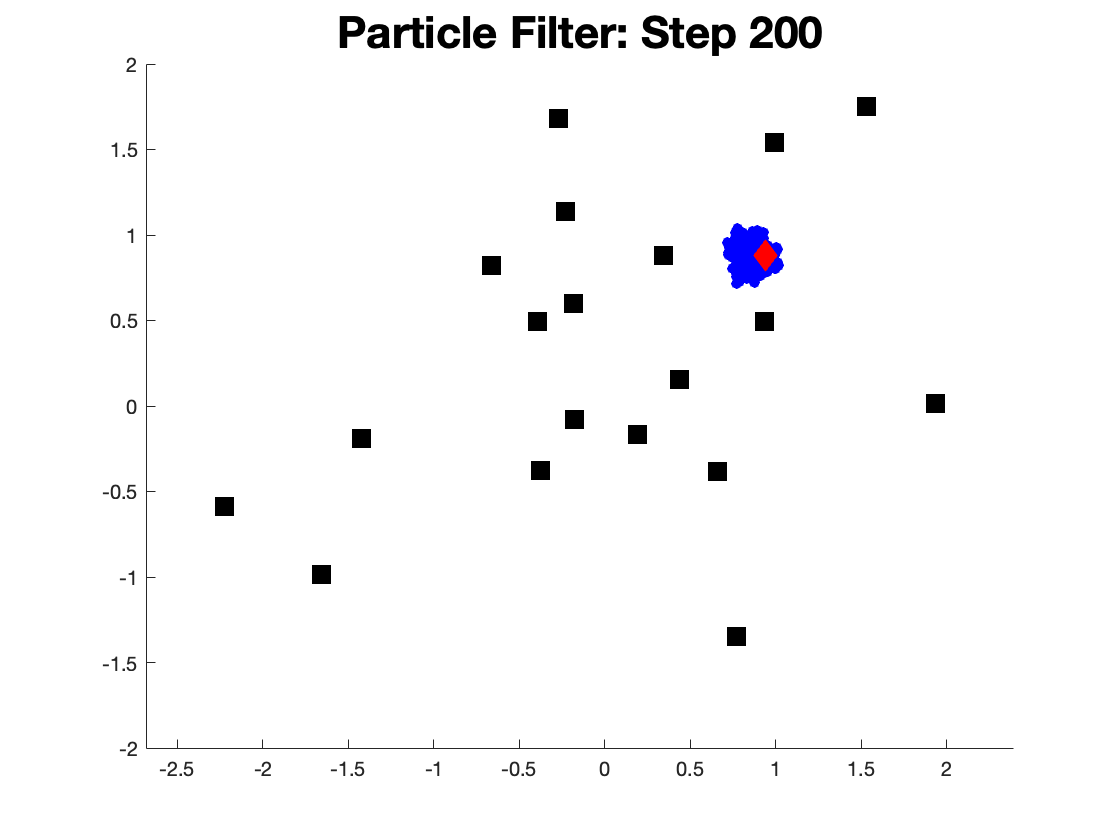
Figure 6.3: Initial estimate of the robot location.

You can play with the code here.

Particle filters have many advantages:

• Ability to approximate non-Gaussian distributions

• Works for any dynamics model and observation model

• Good scalability, they are ``embarassingly parallelizable”

• Easy to implement

However, there are several notable issues with particle filters

• Lack of diversity: over time, especially with uninformative sensor readings, samples tend to congregate (because the resampling step removes particles)

• Measuring Particle Filter performance is difficult

• Particle Filters are non-deterministic

6.4.4 Feedback Particle Filter

(T. Yang, Mehta, and Meyn 2013)

6.5 State Observer

For the system (6.1), let us denote

• \(X(x_0,t_0;t;u)\) the solution at time \(t\) with input \(u\) and initial condition \(x_0\) at time \(t_0\); when \(t_0 = 0\), we write \(X(x_0;t;u)\)

• \(Y(x_0,t_0;t;u)\) the output at time \(t\) with input \(u\) and initial condition \(x_0\) at time \(t_0\), i.e., \(Y(x_0,t_0;t;u) = h(X(x_0,t_0;t;u), u(t))\); when \(t_0 = 0\), we write \(y_{x_0,u}(t)\);

• \(\mathcal{X}_0\) a subset of \(\mathbb{X}\) containing the initial conditions we consider; for any \(x_0 \in \mathcal{X}_0\), we write \(\sigma^+_{\mathcal{X}}(x_0;u)\) the maximal time of existence of \(X(x_0,\cdot;t;u)\) in a set \(\mathcal{X}\)

• \(\mathcal{U}\) the set of all sufficiently many times differentiable inputs \(u: [0,+\infty) \rightarrow \mathbb{U}\).

The problem of state observation is to produce an estimated state \(\hat{x}(t)\) of the true state \(X(x_0,t_0;t;u)\) based on knowledge about the system (6.1) and information about the history of inputs \(u_{[0,t]}\) and outputs \(y_{[0,t]}\), so that \(\hat{x}(t)\) asymptotically converges to \(X(x_0,t_0;t;u)\), for any initial condition \(x_0 \in \mathcal{X}_0\) and any input \(u \in \mathcal{U}\).

There are multiple ways for solving the problem of state observation (see e.g., (Bernard 2019), (Bernard, Andrieu, and Astolfi 2022)). Here we are particularly interested in the approach using a state observer, i.e., a dynamical system whose internal state evolves according to the history of inputs and outputs, from which a state estimation can be reconstructed that guarantees asymptotic convergence to the true state. We formalize this concept below.

Definition 6.1 (State Observer) A state observer for system (6.1) is a couple \((\mathcal{F},\mathcal{T})\) such that

1. \(\mathcal{F}: \mathbb{R}^{l} \times \mathbb{R}^{m} \times \mathbb{R}^d \rightarrow \mathbb{R}^l\) is continuous

2. \(\mathcal{T}\) is a family of continuous functions indexed by \(u \in \mathcal{U}\) where each \(\mathcal{T}_u: \mathbb{R}^l \times [0,+\infty) \rightarrow \mathbb{R}^n\) respects the causality condition \[ \forall \tilde{u}: [0,+\infty) \rightarrow \mathbb{R}^m,\forall t \in [0,+\infty), u_{[0,t]} = \tilde{u}_{[0,t]} \Rightarrow \mathcal{F}_u (\cdot,t) = \mathcal{F}_{\tilde{u}}(\cdot,t). \]

3. For any \(u \in \mathcal{U}\), any \(z_0 \in \mathbb{R}^l\), and any \(x_0 \in \mathcal{X}_0\) such that \(\sigma^+_{\mathbb{X}}(x_0;u) = +\infty\), any solution \(Z(z_0;t;u,y_{x_0,u})\)⁸ to \[\begin{equation} \dot{z} = \mathcal{F}(z,u,y_{x_0,u}) \tag{6.52} \end{equation}\] initialized at \(z_0\) at time \(0\) with input \(u\) and \(y_{x_0,u}\) exists on \([0,+\infty)\) and satisfies \[\begin{equation} \lim_{t \rightarrow \infty} \Vert \hat{X}(x_0,z_0;t;u) - X(x_0;t;u) \Vert = 0, \tag{6.53} \end{equation}\] with \[\begin{equation} \hat{X}(x_0,z_0;t;u) = \mathcal{T}_u(Z(z_0;t;u,y_{x_0,u}),t). \tag{6.54} \end{equation}\] In words, (i) the state observer maintains an internal state (or latent state) \(z \in \mathbb{R}^l\) that evolves according to the latent dynamics \(\mathcal{F}\) in (6.52), where \(u\) and \(y_{x_0,u}\) are inputs; (ii) an estimated state can be reconstructed from the internal state using \(\mathcal{T}_u\) as in (6.54); and (iii) the error between the estimated state and the true state (defined by a proper distance function \(\Vert \cdot \Vert\) on \(\mathbb{X}\)) converges to zero.

If \(\mathcal{T}_u\) is the same for any \(u \in \mathcal{U}\) and is also time independent, then we say \(\mathcal{T}\) is stationary.⁹ In this case, we can simply write the observer (6.52) and (6.54) as \[\begin{equation} \begin{split} \dot{z} &= \mathcal{F}(z,u,y) \\ \hat{x} &= \mathcal{T}(z). \end{split} \tag{6.55} \end{equation}\]

If \(\hat{x}\) can be read off directly from \(z\), then we say the observer (6.55) is in the given coordinates. A special case of this is when \(\hat{x} = z\), i.e., the internal state of the observer is the same as the system state.

6.5.1 General Design Strategy

Theorem 6.1 (Meta Observer) Let \(F: \mathbb{R}^p \times \mathbb{R}^m \times \mathbb{R}^d \rightarrow \mathbb{R}^p\), \(H: \mathbb{R}^p \times \mathbb{R}^m \rightarrow \mathbb{R}^d\) and \(\mathcal{F}: \mathbb{R}^p \times \mathbb{R}^m \times \mathbb{R}^d \rightarrow \mathbb{R}^p\) be continuous functions such that \[\begin{equation} \dot{\hat{\xi}} = \mathcal{F}(\hat{\xi}, u, \tilde{y}) \tag{6.56} \end{equation}\] is an observer for \[\begin{equation} \dot{\xi} = F(\xi,u,H(\xi,u)), \quad \tilde{y} = H(\xi,u), \tag{6.57} \end{equation}\] i.e., for any \(\xi_0,\hat{\xi}_0 \in \mathbb{R}^p\) and any \(u \in \mathcal{U}\), the solution of the observer (6.56), denoted by \(\hat{\Xi}(\hat{\xi}_0;t;u;\tilde{y}_{\xi_0,u})\), and the solution of the true system (6.57), denoted by \(\Xi(\xi_0;t;u)\), satisfy \[\begin{equation} \lim_{t \rightarrow \infty} \Vert \hat{\Xi}(\hat{\xi}_0;t;u;\tilde{y}_{\xi_0,u}) - \Xi(\xi_0;t;u) \Vert = 0. \tag{6.58} \end{equation}\] Note that the observer (6.56) is stationary and in the given coordinates for system (6.57). Indeed the internal state of the observer is the same as the system state.

Now suppose for any \(u \in \mathcal{U}\), there exists a continuous function (i.e., coordinate transformation) \(T_u: \mathbb{R}^n \times \mathbb{R} \rightarrow \mathbb{R}^p\) and a subset \(\mathcal{X}\) of \(\mathbb{X}\) such that

1. For any \(x_0 \in \mathcal{X}_0\) such that \(\sigma^+_{\mathbb{X}}(x_0;u) = + \infty\), \(X(x_0;\cdot;u)\) remains in \(\mathcal{X}\)

2. There exists a concave \(\mathcal{K}\)¹⁰ function \(\rho\) and a positive number \(\bar{t}\) such that \[ \Vert x_a - x_b \Vert \leq \rho (| T_u(x_a,t) - T_u(x_b,t) |), \quad \forall x_a,x_b \in \mathcal{X}, t \geq \bar{t}, \] i.e., \(x \mapsto T_u(x,t)\) becomes injective on \(\mathcal{X}\),¹¹ uniformly in time and space, after a certain time \(\bar{t}\).

3. \(T_u\) transforms the system (6.1) into the system (6.57), i.e., for all \(x \in \mathcal{X}\) and all \(t \geq 0\), we have \[\begin{equation} L_{(f,1)} T_u(x,t) = F(T_u(x,t),u,h(x,u)), \quad h(x,u) = H(T_u(x,t),u), \tag{6.59} \end{equation}\] where \(L_{(f,1)} T_u(x,t)\) is the Lie derivative of \(T_u\) along the vector field \((f,1)\) \[ L_{(f,1)} T_u(x,t) = \lim_{\tau \rightarrow 0} \frac{ T_u (X(x,t;t+\tau;u),t+\tau) - T_u(x,t) }{\tau}. \]

4. \(T_u\) respects the causality condition \[ \forall \tilde{u}: [0,+\infty) \rightarrow \mathbb{R}^m, \forall t \in [0,+\infty), u_{[0,t]} = \tilde{u}_{[0,t]} \Rightarrow T_u(\cdot,t) = T_{\tilde{u}}(\cdot,t). \]

Then, for any \(u \in \mathcal{U}\), there exists a function \(\mathcal{T}_u: \mathbb{R}^p \times [0,+\infty) \rightarrow \mathcal{X}\) (satisfying the causality condition) such that for any \(t \geq \bar{t}\), \(\xi \mapsto \mathcal{T}_u (\xi, t)\) is uniformly continuous on \(\mathbb{R}^p\) and satisfies \[ \mathcal{T}_u \left( T_u(x,t),t \right) = x, \forall x \in \mathcal{X}. \] Moreover, denoting \(\mathcal{T}\) the family of functions \(\mathcal{T}_u\) for \(u \in \mathcal{U}\), the couple \((\mathcal{F}, \mathcal{T})\) is an observer for the system (6.1) initialized in \(\mathcal{X}_0\).

Proof. See Theorem 1.1 in (Bernard 2019).

A simpler version of Theorem 6.1 where the coordinate transformation \(T_u\) is stationary and fixed for all \(u\) is stated below as a corollary.

Corollary 6.7 (Meta Observer with Fixed Transformation) Let \(F: \mathbb{R}^p \times \mathbb{R}^m \times \mathbb{R}^d \rightarrow \mathbb{R}^p\), \(H: \mathbb{R}^p \times \mathbb{R}^m \rightarrow \mathbb{R}^d\) and \(\mathcal{F}: \mathbb{R}^p \times \mathbb{R}^m \times \mathbb{R}^d \rightarrow \mathbb{R}^p\) be continuous functions such that (6.56) is an observer for (6.57).

Suppose there exists a continuous coordinate transformation \(T: \mathbb{R}^p \rightarrow \mathbb{R}^n\) and a compact subset \(\Omega\) of \(\mathbb{R}^n\) such that

1. For any \(x_0 \in \mathcal{X}_0\) such that \(\sigma^+_{\mathbb{X}}(x_0;u) = + \infty\), \(X(x_0;\cdot;u)\) remains in \(\Omega\)

2. \(x \mapsto T(x)\) is injective on \(\Omega\)

3. \(T\) transforms the system (6.1) into system (6.57) \[ L_f T(x) = F(T(x),u,h(x,u)), \quad h(x,u) = H(T(x),u), \] where \(L_f T(x)\) is the Lie derivative of \(T(x)\) along \(f\) \[ L_f T(x) = \lim_{\tau \rightarrow 0} \frac{ T(X(x,t;t+\tau;u)) - T(x)}{\tau}. \]

Then, there exists a uniformly continuous function \(\mathcal{T}:\mathbb{R}^p \rightarrow \mathbb{R}^{n}\) such that \[ \mathcal{T}(T(x)) = x, \quad \forall x \in \Omega, \] and \((\mathcal{F},\mathcal{T})\) is an observer for system (6.1) initialized in \(\mathcal{X}_0\).

Theorem 6.1 and Corollary 6.7 suggest the following general observer design strategy:

1. Find an injective coordinate transformation \(T_u\) (that may be time-varying and also dependent on \(u\)) that transforms the original system (6.1) with coordinate \(x\) into a new system (6.57) with coordinate \(\xi\)

2. Design an observer (6.56), \(\hat{\xi}\), for the new system

3. Compute a left inverse, \(\mathcal{T}_u\), of the transformation \(T_u\) to recover a state estimation \(\hat{x}\) of the original system.

The transformed systems (6.57) are typically referred to as normal forms, or in my opinion, templates.

Of course, the general design strategy is rather conceptual, and in order for it to be practical, we have to answer three questions.

• What templates do we have, what are their associated observers, and what are the conditions for the observers to be asymptotically converging?

• What kinds of (nonlinear) systems can be transformed into the templates, and how to perform the transformation?

• How to invert the coordinate transformation? Is it analytical or does it require numerical approximation?

In the following sections, we will study several representative normal forms and answer the above questions. Before presenting the results, let us first introduce several notions of observability.

Definition 6.2 (Observability) Consider an open subset \(\mathcal{L}\) of the state space \(\mathbb{X} \subseteq \mathbb{R}^n\) of system (6.1). The system (6.1) is said to be

• Distinguishable on \(\mathcal{L}\) for some input \(u(t)\), if for all \((x_a,x_b) \in \mathcal{L} \times \mathcal{L}\), \[ y_{x_a,u}(t) = y_{x_b,u}(t), \forall t \in [0,\min\left\{\sigma^+_{\mathbb{X}}(x_a;u), \sigma^+_{\mathbb{X}}(x_b;u) \right\}] \Longrightarrow x_a = x_b \]

• Instantaneously distinguishable on \(\mathcal{L}\) for some input \(u(t)\), if for all \((x_a,x_b) \in \mathcal{L} \times \mathcal{L}\), and for all \(\bar{t} \in (0, \min\left\{\sigma^+_{\mathbb{X}}(x_a;u), \sigma^+_{\mathbb{X}}(x_b;u) \right\})\), \[ y_{x_a,u}(t) = y_{x_b,u}(t), \forall t \in [0,\bar{t}) \Longrightarrow x_a = x_b \]

• Uniformly observable on \(\mathcal{L}\) if it is distinguishable on \(\mathcal{L}\) for any input \(u(t)\) (not only for \(u \in \mathcal{U}\))

• Uniformly instantaneously observable on \(\mathcal{L}\) if it is instantaneously observable on \(\mathcal{L}\) for any input \(u(t)\) (not only for \(u \in \mathcal{U}\)).

Moreover, let \(\mathcal{X}\) be a subset of \(\mathbb{X}\) such that \(\mathrm{cl}(\mathcal{X})\), i.e., the closure of \(\mathcal{X}\), is contained in \(\mathcal{L}\). Then the system (6.1) is said to be

• Backward \(\mathcal{L}\)-distinguishable on \(\mathcal{X}\) for some input \(u(t)\), if for any \((x_a,x_b) \in \mathcal{X} \times \mathcal{X}\) such that \(x_a \neq x_b\), there exists \(t \in (\max\left\{ \sigma^{-}_{\mathcal{L}}(x_a;u), \sigma^{-}_{\mathcal{L}}(x_b;u) \right\},0]\) such that \(y_{x_a,u}(t) \neq y_{x_b,u}(t)\), or in words similar to the definition of distinguishable on \(\mathcal{L}\), for all \((x_a,x_b) \in \mathcal{X} \times \mathcal{X}\) \[ y_{x_a,u}(t) = y_{x_b,u}(t), \forall t \in (\max\left\{\sigma^{-}_{\mathcal{L}}(x_a;u), \sigma^{-}_{\mathcal{L}}(x_b;u) \right\},0] \Longrightarrow x_a = x_b. \]

6.5.2 Luenberger Template

Consider an instance of the normal form (6.57) as follows: \[\begin{equation} \dot{\xi} = A \xi + B(u,y), \quad y = C \xi, \tag{6.60} \end{equation}\] where \(A,C\) are constant matrices, and \(B(u,y)\) can depend nonlinearly on \(u\) and \(y\).

For this template, we have the well-known Luenberger observer.

Theorem 6.2 (Luenberger Observer) If the pair \((A,C)\) is detectable (see Theorem C.9), then there exists a matrix \(K\) such that \(A-KC\) is Hurwitz and the system \[\begin{equation} \dot{\hat{\xi}} = A \hat{\xi} + B(u,y) + K(y - C \hat{\xi}) \tag{6.61} \end{equation}\] is an observer for (6.60).

Proof. Define \(e(t) = \xi(t) - \hat{\xi}(t)\). In that case, \[\begin{equation} \dot{e}(t) = [A - KC] e(t) \tag{6.62} \end{equation}\]

Solving (6.62), we obtain

\[\begin{equation} e(t) = \mathrm{exp}[(A - KC)t] e(0) \end{equation}\]

Then, if the real components of the eigenvalues of \(A - KC\) are strictly negative (i.e., \(A - KC\) is Hurwitz), then \(e(t) \rightarrow 0\) as \(t \rightarrow \infty\), independent of the initial error \(e(0) = \xi(0) - \hat{\xi}(0)\). From Theorem C.9, we know that \((A,C)\) being detectable implies the existence of \(K\) such that \(A - KC\) is Hurwitz.

If one is further interested in estimating the convergence rate of the Luenberger observer, then one can use the result from Corollary C.1. Particularly, one can solve the Lyapunov equation \[ (A - KC)^T P + P (A - KC) = - I \] to obtain \(P\). Then the convergence rate of \(\Vert e \Vert\) towards zero is \(\frac{0.5}{\lambda_{\max}(P)}\).

The Luenberger observer is an elegant result in observer design (and even in control theory) that has far-reaching impact. In my opinion, the essence of observer design is twofold: (i) to simulate the dynamics when the state estimation is correct, and (ii) to correct the state estimation from observation when it is off. These two pieces of ideas are evident in (6.61): the observer is a copy of the original dynamics (\(A \hat{\xi} + B(u,y)\)) plus a feedback correction from the difference between the “imagined” observation \(C\hat{\xi}\) and the true observation \(y\).

You may think the Luenberger template is restricting because it requires the system to be linear (up to the only nonlinearly in \(B(u,y)\)). However, it turns out the Luenberger template is already quite useful, as I will show in the following pendulum example.

Example 6.3 (Luenberger Observer for A Simple Pendulum) Consider a simple pendulum dynamics model \[\begin{equation} x = \begin{bmatrix} \theta \\ \dot{\theta} \end{bmatrix}, \quad \dot{x} = \begin{bmatrix} \dot{\theta} \\ - \frac{1}{ml^2} (b \dot{\theta} + mgl \sin \theta) \end{bmatrix} + \begin{bmatrix} 0 \\ \frac{1}{ml^2} \end{bmatrix} u, \quad y = \theta, \tag{6.63} \end{equation}\] where \(\theta\) the angular position of the pendulum from the vertical line, \(m > 0\) the mass of the pendulum, \(l > 0\) the length, \(g\) the gravitational constant, \(b > 0\) the dampling coefficient, and \(u\) the control input (torque).

We assume we can only observe the angular position of the pendulum in (6.63), e.g., using a camera, but not the angular velocity. Our goal is to construct an observer that can provide a full state estimation.

We first note that the pendulum dynamics (6.63) can actually be written in the (linear) Luenberger template (6.60) as¹² \[\begin{equation} \begin{split} \dot{x} & = \underbrace{\begin{bmatrix} 0 & 1 \\ 0 & - \frac{b}{ml^2} \end{bmatrix}}_{=:A} x + \underbrace{\begin{bmatrix} 0 \\ \frac{u - mgl \sin \theta }{ml^2} \end{bmatrix}}_{=:B(u,y)} \\ y & = \underbrace{\begin{bmatrix} 1 & 0 \end{bmatrix}}_{=:C} x \end{split}. \tag{6.64} \end{equation}\]

In order for us to use the Luenberger observer, we need to check if the pair \((A,C)\) is detectable. We can easily find the eigenvalues and eigenvectors of \(A\): \[ A \begin{bmatrix} 1 \\ 0 \end{bmatrix} = 0,\quad A \begin{bmatrix} - \frac{ml^2}{b} \\ 1 \end{bmatrix} = \begin{bmatrix} 1 \\ - \frac{b}{ml^2} \end{bmatrix} = - \frac{b}{ml^2} \begin{bmatrix} - \frac{ml^2}{b} \\ 1 \end{bmatrix}. \] The first eigenvalue has real part equal to \(0\). However, \[ C \begin{bmatrix} 1 \\ 0 \end{bmatrix} = 1 \neq 0. \] According to Theorem C.9, we conclude \((A,C)\) is detectable. In fact, the pair \((A,C)\) is more than just detectable, it is indeed observable (according to Theorem C.7). Therefore, the poles of \(A - KC\) can be arbitrarily placed.

Finding \(K\). Now we need to find \(K\). An easy choice of \(K\) is \[ K = \begin{bmatrix} k \\ 0 \end{bmatrix}, \quad A - KC = \begin{bmatrix} - k & 1 \\ 0 & - \frac{b}{ml^2} \end{bmatrix}. \] With \(k > 0\), we know \(A- KC\) is guaranteed to be Hurwitz (the two eigenvalues of \(A-KC\) are \(-k\) and \(-b/ml^2\)), and we have obtained an observer!

We can also estimate the convergence rate of this observer. Let us use \(m=1,g=9.8,l=1,b=0.1\) as parameters of the pendulm dynamics. According to Theorem 6.2, we solve the Lyapunov equation \[ (A - KC)^T P + P(A - KC) = -I \] and \(\gamma = \frac{0.5}{\lambda_{\max}(P)}\) will be our best estimate of the convergence rate (of \(\Vert e \Vert = \Vert \hat{x} - x \Vert\) towards zero).

Table 6.1 below shows the convergence rates computed for different values of \(k\). We can see that as \(k\) is increased, the convergence rate estimation is also increased. However, it appears that \(0.1\) is the best convergence rate we can achieve, regardless of how large \(k\) is.

Table 6.1: Convergence rate estimation of the Luenberger observer for a simple pendulm.

\(k\)	\(0.1\)	\(1\)	\(10\)	\(100\)	\(1000\)	\(10000\)
\(\gamma\)	\(0.0019\)	\(0.0523\)	\(0.0990\)	\(0.1000\)	\(0.1000\)	\(0.1000\)

Optimal \(K\). Is it true that \(0.1\) is the best convergence rate, or in other words, what is the best \(K\) that maximizes the convergence rate \(\gamma\)?

A natural way (and my favorite way) to answer this question is to formulate an optimization problem. \[\begin{equation} \begin{split} \min_{P,K} & \quad \lambda_{\max}(P) \\ \text{subject to} & \quad (A - KC)^T P + P (A - KC) = -I \\ & \quad P \succeq 0 \end{split} \tag{6.65} \end{equation}\] The above formulation seeks the best possible \(K\) that minimizes \(\lambda_{\max}(P)\) which, according to \(\gamma = 0.5 / \lambda_{\max}(P)\), also maximizes \(\gamma\).

However, problem (6.65) is not a convex formulation due to the bilinear term \(PK\). Nevertheless, via a simple change of variable \(H = PK\), we arrive at the following convex formulation \[\begin{equation} \begin{split} \min_{P,H} & \quad \lambda_{\max}(P) \\ \text{subject to} & \quad A^T P - C^T H^T + PA - H C = - I \\ & \quad P \succeq 0 \end{split} \tag{6.66} \end{equation}\] Problem (6.66) is a semidefinite programming problem (SDP), that can be modeled and solved by off-the-shelf tools. We can recover \(K = P^{-1} H\) from (6.66) after it is solved.

Interestingly, solving problem (6.66) verifies that the minimum \(\lambda_{\max}(P)\) is \(5\) and the maximum converge rate is \(0.1\). An optimal solution of (6.66) is \[ P^\star = \begin{bmatrix} 2.4923 & 0 \\ 0 & 5 \end{bmatrix}, \quad K^\star = \begin{bmatrix} 0.2006 \\ 0.4985 \end{bmatrix}. \] You should check out the Matlab code of this example here.

6.5.3 State-affine Template

Consider an instance of the normal form (6.57) where the dynamics is linear in \(\xi\), but the coefficients are time-varying and dependent on the input and output \[\begin{equation} \dot{\xi} = A(u,y) \xi + B(u,y), \quad y = C(u) \xi. \tag{6.67} \end{equation}\] The difference between the state-affine template (6.67) and the Luenberger template (6.60) is that the linear matrices \(A,C\) are allowed to depend nonlinearly on the input \((u,y)\).

Kalman and Bucy originally proposed an observer for linear time-varying systems (Rudolph E. Kalman and Bucy 1961). The result is later extened by (Besançon, Bornard, and Hammouri 1996) and (Hammouri and Leon Morales 1990) to deal with coefficient matrices dependent on the control. The following theorem is a direct extension of the result from (Besançon, Bornard, and Hammouri 1996) and (Hammouri and Leon Morales 1990) by considering \((u,y)\) as an augmented control input.

Before presenting the theorem, we need to introduce the following terminology.

Definition 6.3 (Linear Time-Varying System) For a linear time-varying system of the form \[\begin{equation} \dot{\chi} = A(\nu) \chi, \quad y = C(\nu) \chi, \tag{6.68} \end{equation}\] with input \(\nu\) and output \(y\), we define

• the transition matrix \(\Psi_\nu\) as the unique solution to \[ \Psi_\nu (t,t) = I, \quad \frac{\partial \Psi_\nu}{\partial \tau}(\tau,t) = A(\nu(\tau)) \Psi_\nu (\tau, t). \] Note that the transition matrix is used to express the solution to (6.68) because it satisfies \[ \chi(\chi_0,t_0;t;\nu) = \Psi_\nu (t,t_0) \chi_0. \]

• the observability grammian as \[ \Gamma_\nu (t_0,t_1) = \int_{t_0}^{t_1} \Psi_\nu (\tau,t_0)^T C(\nu(\tau))^T C(\nu(\tau)) \Psi_\nu (\tau,t_0) d\tau. \]

• the backward observability grammian as \[ \Gamma_\nu^b (t_0,t_1) = \int_{t_0}^{t_1} \Psi_\nu (\tau,t_1)^T C(\nu(\tau))^T C(\nu(\tau)) \Psi_\nu (\tau,t_1) d\tau. \]

We now introduce the Kalman-Bucy Observer for the state-affine template (6.67).

Theorem 6.3 (Kalman-Bucy Observer) Let \(y_{\xi_0,u}(t) = C(u(t)) \Xi (\xi_0;t;u)\) be the output of system (6.67) at time \(t\) with initialization \(\xi_0\) and control \(u\). Suppose the control \(u\) satisfies

• For any \(\xi_0\), \(t \mapsto A(u(t),y_{\xi_0,u}(t))\) is bounded by \(A_{\max}\)

• For any \(\xi_0\), the augmented input \(\nu = (u,y_{\xi_0,u})\) is regularly persistent for the dynamics \[\begin{equation} \dot{\chi} = A(\nu) \chi , \quad y = C(\nu) \chi \tag{6.69} \end{equation}\] uniformly with respect to \(\xi_0\). That is, there exist strictly positive numbers \(t_0,\bar{t}\), and \(\alpha\) such that for any \(\xi_0\) and any time \(t \geq t_0 \geq \bar{t}\), \[ \Gamma_v^b (t-\bar{t}, t) \succeq \alpha I, \] where \(\Gamma_v^b\) is the backward observability grammian associated with system (6.69).

Then, given any positive definite matrix \(P_0\), there exist \(\alpha_1,\alpha_2 > 0\) such that for any \(\lambda \geq 2 A_{\max}\) and any \(\xi_0 \in \mathbb{R}^p\), the matrix differential equation \[\begin{equation} \dot{P} = -\lambda P - A(u,y)^T P - P A(u,y) + C(u)^T C(u) \tag{6.70} \end{equation}\] initialized at \(P(0) = P_0\) admits a unique solution satisfying \(P(t)=P(t)^T\) and \[ \alpha_2 I \succeq P(t) \succeq \alpha_1 I. \] Moreover, the system \[\begin{equation} \dot{\hat{\xi}} = A(u,y) \hat{\xi} + B(u,y) + K (y - C(u)\hat{\xi}) \tag{6.71} \end{equation}\] with a time-varying gain matrix \[\begin{equation} K = P^{-1} C(u)^T \tag{6.72} \end{equation}\] is an observer for the state-affine system (6.67).

Let us work out an example of the Kalman-Bucy Observer for nonlinear systems.

Example 6.4 (Kalman-Bucy Observer for A Simple Pendulum) Let us reconsider the pendulum dynamics (6.63) but this time try to design a Kalman-Bucy observer.

We first write the pendulum dynamics in a new coordinate system so that it is in the state-affine normal form (6.67). We choose \(\xi = [\mathfrak{s},\mathfrak{c},\dot{\theta}]^T\) with \(\mathfrak{s} = \sin \theta\) and \(\mathfrak{c} = \cos \theta\). Clearly, we will be able to observe \(y = [\mathfrak{s},\mathfrak{c}]^T\) in this new coordinate. The state-affine normal form of the pendulum dynamics reads \[\begin{equation} \begin{split} \dot{\xi} = \begin{bmatrix} \mathfrak{c} \dot{\theta} \\ - \mathfrak{s} \dot{\theta} \\ - \frac{1}{ml^2} (b \dot{\theta} + mgl \mathfrak{s} ) + \frac{1}{ml^2} u \end{bmatrix} & = \underbrace{\begin{bmatrix} 0 & 0 & \mathfrak{c} \\ 0 & 0 & -\mathfrak{s} \\ 0 & 0 & -\frac{b}{ml^2} \end{bmatrix}}_{=:A(u,y)} \xi + \underbrace{\begin{bmatrix} 0 \\ 0 \\ \frac{u - mgl \mathfrak{s}}{ml^2} \end{bmatrix}}_{=:B(u,y)} \\ y & = \underbrace{\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \end{bmatrix}}_{=:C(u)} \xi \end{split}. \tag{6.73} \end{equation}\] Note that \(C(u)\) is in fact time-invariant, and \(B(u,y)\) only depends on \(u\); but we adopt the same notation as the general state-affine template (6.67).

In order to use the Kalman-Bucy observer in Theorem 6.3, we need to verify the boundedness of \(A(u,y)\), and the regular persistence of (6.69).

Boundedness of \(A(u,y)\). We can easily show the boundedness of \(A(u,y)\) by writing \[ \Vert A(u,y) \xi \Vert = \Vert \xi_3 (\mathfrak{c} - \mathfrak{s} - b/ml^2) \Vert \leq |\xi_3| \sqrt{3} \sqrt{\mathfrak{c}^2 + \mathfrak{s}^2 + b^2 / m^2 l^4} \leq \Vert \xi \Vert \sqrt{3 + 3b^2 / m^2 l^4}. \] Therefore, we can take \(A_{\max} = \sqrt{3 + 3b^2 / m^2 l^4}\).

Regular persistence. We write the backward observability grammian of system (6.69) \[ \Gamma_\nu^b(t - \bar{t},t) = \int_{t - \bar{t}}^t \Psi_\nu(\tau,t)^T C^T C \Psi_\nu (\tau, t) d \tau = \int_{t - \bar{t}}^t \Psi_\nu(\tau,t)^T \underbrace{\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{bmatrix}}_{=:\tilde{C}} \Psi_\nu (\tau, t) d \tau. \] \(\Gamma_\nu^b(t - \bar{t},t) \succeq \alpha I\) if and only if \[ w^T \Gamma_\nu^b(t - \bar{t},t) w \geq \alpha, \quad \forall w \in \mathbb{R}^3, \Vert w \Vert = 1. \] With this, we develop \(w^T \Gamma_\nu^b(t - \bar{t},t) w\) \[\begin{equation} \begin{split} w^T \Gamma_\nu^b(t - \bar{t},t) w &= \int_{t - \bar{t}}^t s^T \tilde{C} s d\tau, \\ & = \int_{t - \bar{t}}^t \left( s_1^2 + s_2^2 \right) d\tau, \quad s = \Psi_\nu (\tau, t) w \end{split} \tag{6.74} \end{equation}\] and observe that \(s = \Psi_\nu (\tau,t) w\) is equivalent to \[ w = (\Psi_\nu (\tau,t))^{-1} s = \Psi_\nu (t,\tau) s, \] that is, \(w\) is the solution of \(\dot{\xi} = A(\nu) \xi\) at time \(t\) with initial condition \(s\) at time \(\tau \leq t\). Equivalently, this is saying \(s\) is the initial condition of \(\dot{\xi} = A(\nu) \xi\) at time \(\tau \leq t\) such that its solution at time \(t\) is \(w\). Note that from (6.74) it is clearly that \(\int_{t - \bar{t}}^t \left( s_1^2 + s_2^2 \right) d\tau \geq 0\), and \(\int_{t - \bar{t}}^t \left( s_1^2 + s_2^2 \right) d\tau = 0\) if and only if \(s_1^2 + s_2^2 = 0\), or equivalently \(s_1 = s_2 = 0\) for any \(\tau \in [t - \bar{t}, t]\).

We then take a closer look at the system \(\dot{\xi} = A(\nu) \xi\): \[\begin{equation} \begin{split} \dot{\xi}_1 &= \mathfrak{c} \xi_3 \\ \dot{\xi}_2 &= -\mathfrak{s} \xi_3 \\ \dot{\xi}_3 &= - \frac{b}{ml^2} \xi_3. \end{split} \tag{6.75} \end{equation}\]

If the solution of \(\xi_3\) at time \(t\) is \(w_3\), then \[ \xi_3(\tau) = w_3 e^{\frac{b}{ml^2}(t - \tau)}, \quad \tau \leq t. \] We can now claim it is impossible that \(s_1 = s_2 = 0\) at any time \(\tau \in [t - \bar{t}, t]\).

We can show this by contradiction. First of all, \(s_1 = s_2 = 0\) at \(\tau = t\) implies \(w_1 = w_2 = 0\) and hence \(w_3 = \pm 1\). This implies \(\xi_3 \neq 0\) for any \(\tau \in [t - \bar{t}, t]\). Then, \(s_1 = 0, \forall \tau \in [t - \bar{t}, t]\) implies \(\dot{\xi}_1 = 0\) which, due to \(\xi_3 \neq 0\), implies \(\mathfrak{c} = 0\) for all \(\tau\). Similarly, \(s_2 = 0, \forall \tau \in [t - \bar{t}, t]\) implies \(\dot{\xi}_2 = 0\) and \(\mathfrak{s} = 0\). This creates a contradiction because \(\mathfrak{c}^2 + \mathfrak{s}^2 = 1\) and \(\mathfrak{c}, \mathfrak{s}\) cannot be simultaneously zero.

The above reasoning proves that the backward observability Grammian is positive definite, which is, however, still insufficient for the Kalman-Bucy observer. We need a stronger uniformly positive definite condition on \(\Gamma_\nu^b\), i.e., to find \(t_0, \bar{t}\) and \(\alpha>0\) so that \(\Gamma_\nu^b(t-\bar{t},t) \succeq \alpha I\) for all \(t \geq t_0\).

If the control \(u\) is unbounded, then sadly, one can show that the uniform positive definite condition fails to hold, as left by you to show in the following exercise.

Exercise 6.1 (Counterexample for Kalman-Bucy Observer) Show that, if the control \(u\) is unbounded, then for any \(\alpha > 0\), \(t_0 \geq \bar{t} > 0\), there exists \(t \geq t_0\) such that \(\Gamma_\nu^b(t - \bar{t},t) \prec \alpha I\). (Hint: consider a controller that spins the pendulum faster and faster such that in time \(\bar{t}\) it has rotated \(2k\pi\), in this case the angular velocity becomes unobservable because we are not sure how many rounds the pendulum has rotated.)

Fortunately, if the control \(u\) is bounded, then we can prove the uniform positive define condition holds for \(\Gamma_\nu^b(t - \bar{t},t)\). The following proof is given by Weiyu Li.

Without loss of generality, let \(\frac{b}{ml^2} = 1\). Assume \(u\) is bounded such that the third entry of \(B(u,y)\) in (6.73) is bounded by \(\beta > 0\) \[ \left| \frac{u - mgl \mathfrak{s}}{ml^2} \right| \leq \beta. \] Assuming the initial velocity of the pendulum is \(\dot{\theta}(0) = \dot{\theta}_0\), we know \(\dot{\theta}(t)\) is bounded by \[ \dot{\theta}(t) \in \left[ c_1(1-\beta)e^{-t} - \beta , c_2(1-\beta)e^{-t} + \beta \right], \] where \(c_1,c_2\) are constants chosen to satisfy the initial condition. Clearly, for all \(t > 0\), we see \(\dot{\theta}(t)\) is bounded, and hence we know \(\dot{\mathfrak{c}}\) and \(\dot{\mathfrak{s}}\) are bounded (due to \(\mathfrak{c}\) and \(\mathfrak{s}\) are bounded). Intuitively, what we have just shown says that when the control is bounded, the measurements \(\mathfrak{c}\) and \(\mathfrak{s}\) will have bounded time derivatives. (This will help us analyze the auxiliary system (6.75).)

Now back to checking regular persistence of the auxilary system (6.75). We will discuss two cases: (1) \(w_3^2 > 1 - \delta\), and (2) \(w_3^2 \leq 1 - \delta\), for some constant \(\delta < 0.5\) determined later.

1. \(w_3^2 > 1 - \delta > 0.5\). In this case we have \(w_1^2 + w_2^2 = 1 - w_3^2 < \delta\), and hence \(w_1^2 < \delta\), \(w_2^2 < \delta\). On the other hand, from (6.75) we have \[ \dot{\xi}_1^2(\tau) + \dot{\xi}_2^2(\tau) = \xi_3^2 = w_3^2 e^{2 (t - \tau)} > w_3^2 > 1 - \delta, \quad \forall \tau < t. \] Without loss of generality assume \(\dot{\xi}_1(t)^2 > (1-\delta)/2\). As \(\dot{\xi}_1 = \mathfrak{c} \xi_3\) and both \(\mathfrak{c}\) and \(\xi_3\) have bounded derivatives, we know \(\dot{\xi}_1\) will not change sign for some duration \(T\) that is independent from the choice of \(\delta\) (because the time derivatives of \(\mathfrak{c}\) and \(\xi_3\) do not depend on \(\delta\)). That is \(|\dot{\xi}_1| > \sqrt{(1-\delta)/2} > 1/2\) for \(\tau \in [t - T,t]\). Consequently, \[ |\xi_1(t - \tau)| > \frac{1}{2} \tau - |w_1| > \frac{1}{2} \tau - \sqrt{\delta}, \quad \tau \in [0,T]. \] Choosing \(\delta\) small enough, we have \(|\xi_1(t - \tau)| > 0.25 \tau\) for \(\tau \in [0.5T,T]\). Then we have \[ \Gamma_\nu^b(t - T, t) \succ [(0.25 \times 0.5 T)^2 \times 0.5T]I. \]

2. \(w_3^2 \leq 1-\delta\). In this case \(w_1^2 + w_2^2 = 1 - w_3^2 \geq \delta\), and at least one of \(w_1\) and \(w_2\) has absolute value larger than \(\sqrt{\delta/2}\). Because the derivatives of \(\xi_1\) and \(\xi_2\) are both bounded, we know \(\xi_1\) and \(\xi_2\) will remain large for some constant time. Thus there is a uniform lower bound.

The intuition of the above proof is simple: when \(\xi_1\) and/or \(\xi_2\) already have large absolute value (case 2), we can find a time window such that \(\xi_1\) and/or \(\xi_2\) remain large in that time window; when \(\xi_1\) and/or \(\xi_2\) are small (case 1), using the observation that their time derivatives are large (because \(w_3\) is large), together with the fact that these derivatives remain large (because the derivative of these derivatives are bounded), we can also find a time window that \(\xi_1\) and/or \(\xi_2\) are large (back in time). Therefore, the backward observability Grammian is uniformly positive definite.

6.5.4 Kazantzis-Kravaris-Luenberger (KKL) Template

In Luenberger’s original paper about observer design for linear systems (Luenberger 1964), the goal was to transform a linear system \[ \dot{x} = F x, \quad y = C x \] into a Hurwitz form \[\begin{equation} \dot{\xi} = A \xi + B y \tag{6.76} \end{equation}\] with \(A\) a Hurwitz (stable) matrix. If such a transformation is available, then the following system \[ \dot{\hat{\xi}} = A \hat{\xi} + B y, \] which is nothing but a copy of the dynamics (6.76), is in fact an observer. This is because the error \(e = \hat{\xi} - \xi\) evolves as \[ \dot{e} = A e, \] which implies that \(e\) tends to zero regardless of the initial error \(e(0)\). Luenberger proved that when \((F,C)\) is observable, a stationary transformation \(\xi = T x\) with \(p = n\), i.e., \(T \in \mathbb{R}^{n\times n}\), always exists and is unique, for any matrix \(A\) that is Hurwitz and \((A,B)\) that is controllable. This is based on the fact that \[\begin{align} (A T + B C) x =A \xi + B y =\dot{\xi} = T \dot{x} = TF x, \forall x \\ \Longleftrightarrow AT + BC = TF, \end{align}\] known as the Sylvester equation, admits a unique and invertible solution \(T\).

A natural extension of Luenberger’s original idea is to find a transformation that converts the nonlinear system (6.1) into the following form \[\begin{equation} \dot{\xi} = A \xi + B(u,y), \quad y = H(\xi,u), \tag{6.77} \end{equation}\] with \(A\) a Hurwitz matrix (but \(H\) can be nonlinear, as opposed to the Luenberger template in Theorem 6.2). If such a transformation can be found, then we can design a similar observer that copies the dynamics (6.77) \[\begin{equation} \dot{\hat{\xi}} = A \hat{\xi} + B(u,y). \tag{6.78} \end{equation}\] We refer to such a nonlinear Luenberger template the Kazantzis-Kravaris-Luenberger (KKL) template, due to the seminal work (Kazantzis and Kravaris 1998).

The KKL template, once found, is nice in the sense that (i) the observer (6.78) is a simple copy of the dynamics and also very easy to implement (as opposed to the Kalman-Bucy observer); and (ii) checking if the matrix \(A\) is Hurwitz is easy, at least when \(A\) has reasonable size, (e.g., compared to checking the regular persistence condition in the state-affine template in Theorem 6.3).

However, the KKL template is difficult to realize in the sense that (i) what kind of nonlinear systems can be converted to (6.77), and (ii) for those systems, how do we find the coordinate transformation?

Recent works have leveraged deep learning to learn the coordinate transformation, for example in (Janny et al. 2021), (Niazi et al. 2023), (Miao and Gatsis 2023). Before hammering the problem with deep learning, let us look at the fundamentals of the KKL observer.

6.5.4.1 Autonomous Systems

Consider the autonomous version of system (6.1) without control \[\begin{equation} \dot{x} = f(x), \quad y = h(x), \tag{6.79} \end{equation}\] where \(x \in \mathbb{X} \subseteq \mathbb{R}^n, y \in \mathbb{Y} \subseteq \mathbb{R}^d\).

The following result, established by (Andrieu and Praly 2006), states that the KKL observer exists under mild conditions.

Theorem 6.4 (KKL Observer for Autonomous Systems) Assum \(\mathcal{X}\) and \(\mathcal{L}\) are open bounded sets in \(\mathbb{X}\) (the state space) such that \(\mathrm{cl}(\mathcal{X})\) is contained in \(\mathcal{L}\) and the system (6.79) is backward \(\mathcal{L}\)-distinguishable on \(\mathcal{X}\) (cf. Definition 6.2). Then there exists a strictly positive number \(\gamma\) and a set \(\mathcal{S}\) of zero Lebesgue measure in \(\mathbb{C}^{n+1}\) such that denoting \(\Omega = \{ \lambda \in \mathbb{C} \mid \mathrm{Re}(\lambda) < - \gamma \}\), for any \((\lambda_1,\dots,\lambda_{n+1}) \in \Omega^{n+1} \backslash \mathcal{S}\), there exists a function \(T: \mathbb{R}^n \rightarrow \mathbb{R}^{(n+1)d}\) uniformly injective on \(\mathcal{X}\) satisfying \[ L_f T(x) = A T(x) + B(h(x)) \] with \[\begin{align} A = \tilde{A} \otimes I_d, \quad B(y) = (\tilde{B} \otimes I_d ) y \\ \tilde{A} = \begin{bmatrix} \lambda_1 & & \\ & \ddots & \\ & & \lambda_{n+1} \end{bmatrix} \quad \tilde{B} = \begin{bmatrix} 1 \\ \vdots \\ 1 \end{bmatrix}. \end{align}\] Moreover, if \(\mathcal{X}\) is backward invariant, then \(T\) is unique and defined by \[\begin{equation} T(x) = \int_{-\infty}^0 e^{-A\tau} B(h(X(x,\tau))) d\tau. \tag{6.80} \end{equation}\]

Remark. The function \(T\) in Theorem 6.4 takes complex numbers. To simulate the observer \[ \dot{\hat{\xi}} = A \hat{\xi} + B(y), \] one needs to implement in real numbers, for each \(\lambda_i\) and \(j \in [d]\) \[ \dot{\hat{\xi}}_{\lambda_i,j} = \begin{bmatrix} - \mathrm{Re}(\lambda_i) & - \mathrm{Im}(\lambda_i) \\ \mathrm{Im}(\lambda_i) & - \mathrm{Re}(\lambda_i) \end{bmatrix} \hat{\xi}_{\lambda_i,j} + \begin{bmatrix} y_j \\ 0 \end{bmatrix}. \] Therefore, the dimension of the observer is \(2 \times d (n+1)\).

Theorem 6.4 states that as long as the system (6.79) is backward distinguishable, then there exists a stationary transformation \(T\) that can transform the system to a new coordinate system \(\xi\) such that the dynamics in \(\xi\) is Hurwitz. A closer look at the structure of \(A\) and \(B\) reveals that the coordinate transformation needs to satisfy \(n+1\) differential equations of the form \[ \frac{\partial T_{\lambda}}{\partial x}(x) \dot{x} = \lambda T_{\lambda} (x) + y \] where each \(T_{\lambda}\) transforms the state \(x\) into a new coordinate having the same dimension of \(y\). Clearly, if \(T = (T_\lambda)\), i.e., there is a single \(\lambda\), then \(T\) is not uniformly injective (as the dimension of \(\xi\) is \(d < n\)). Consequently, by choosing \[ T = (T_{\lambda_1},\dots,T_{\lambda_{n+1}}), \] the uniform injectivity of \(T\) is ensured.

However, the difficulty lies in the computation of \(T\) (and \(T_\lambda\)), let alone its inverse (that recovers \(x\) from \(\xi\)). Even though \(\mathcal{X}\) is backward invariant, the formulation (6.80) is difficult to compute. I tried very hard to find a coordinate transformation \(T\) that can convert the non-controlled pendulum dynamics into the KKL form but did not succeed. You should let me know if you were able to find one! Nevertheless, the following example shows you the flavor of how such a transformation may look like for a different system.

Example 6.5 (KKL Observer for an Oscillator with Unknown Frequency) Consider a harmonic oscillator with unknown frequency \[ \begin{cases} \dot{x}_1 = x_2 \\ \dot{x}_2 = - x_1 x_3 \\ \dot{x}_3 = 0 \end{cases}, \quad y = x_1 \] Consider the coordinate transformation \[ T_{\lambda_i} (x) = \frac{\lambda_i x_1 - x_2}{\lambda_i^2 + x_3}, \quad \lambda_i > 0, i=1,\dots,p. \] We have \[\begin{align} \frac{\partial T_{\lambda_i}(x)}{\partial x} \dot{x} &= \left\langle \begin{bmatrix} \frac{\lambda_i}{\lambda_i^2 + x_3} \\ \frac{-1 }{\lambda_i^2 + x_3} \\ \frac{x_2 - \lambda_i x_1}{(\lambda_i^2 + x_3)^2} \end{bmatrix}, \begin{bmatrix} x_2 \\ -x_1 x_3 \\ 0 \end{bmatrix} \right \rangle = \frac{\lambda_i x_2 + x_1 x_3}{\lambda_i^2 + x_3} \\ -\lambda_i T_{\lambda_i}(x) + y &= \frac{-\lambda_i^2 x_1 + \lambda_i x_2 + x_1 \lambda_i^2 + x_1 x_3}{\lambda_i^2 + x_3} = \frac{\lambda_i x_2 + x_1 x_3}{\lambda_i^2 + x_3} \end{align}\] Therefore, with \[ \xi = T(x) = [T_{\lambda_1}(x), T_{\lambda_2}(x),\dots,T_{\lambda_p}(x)]^T, \] we have \[ \dot{\xi} = \underbrace{\begin{bmatrix} - \lambda_1 & & \\ & \ddots & \\ & & -\lambda_p \end{bmatrix}}_{A} \xi + \begin{bmatrix}1 \\ \vdots \\ 1 \end{bmatrix} y \] with \(A\) clearly Hurwitz.

With some extra arguments (cf. Section 8.1.1 in (Bernard 2019)), one can see that the transformation \(T\) is injective with \(p \geq 4\) distinct \(\lambda_i\)’s. Therefore, this is a valid KKL observer.

The final issue that one needs to think about is, since the observer is estimating \(\hat{\xi}\), how to recover \(\hat{x}\)? In this example, there is actually no analytical formula for recovering \(\hat{x}\) from \(\hat{\xi}\). In this case, one approach is to solve the following optimization problem \[ \hat{x} = \arg\min_{x} \Vert \hat{\xi} - T(x) \Vert^2, \] which may be quite expensive.

A more general treatment is given in Section 8.2.2 in (Bernard 2019).

6.5.4.2 Controlled Systems

6.5.5 Triangular Template

6.5.6 Design with Convex Optimization

Consider a nonlinear system \[\begin{equation} \dot{x} = f(x) + \psi(u,y), \quad y = Cx \tag{6.81} \end{equation}\] where \(x \in \mathbb{X} \subseteq \mathbb{R}^n\), \(y \in \mathbb{R}^d\), \(C\) a constant matrix, and \(\psi(u,y)\) a nonlinear function. We assume that \(f(x)\) is a polynomial vector map (i.e., each entry of \(f\) is a polynomial function in \(x\)). Certainly the formulation in (6.81) is not as general as (6.1), but it is general enough to include many examples in robotics.

Recall that I said the essence of observer design is to (i) simulate the dynamics when the state estimation is correct, and (ii) to correct the state estimation from observation when it is off. Therefore, we wish to design an observer for (6.81) in the following form \[\begin{equation} \dot{\hat{x}} = \underbrace{f(\hat{x}) + \psi(u,y)}_{\text{dynamics simulation}} + \underbrace{K(y - \hat{y},y)(C \hat{x} - y)}_{\text{feedback correction}}, \tag{6.82} \end{equation}\] where, compared to the Luenberger observer (6.61), we allow the gain matrix \(K\) to be nonlinear functions of the true observation \(y\) and the estimated observation \(\hat{y}\).

With the observer (6.82), the dynamics on the estimation error \(e = \hat{x} - x\) becomes \[ \dot{e} = f(x + e) - f(x) + K(Ce,Cx)C e. \]

If we can find a Lyapunov-like function \(V(e)\) so that \(V(e)\) is positive definite and \(\dot{V}(e)\) is negative definite, then Lyapunov stability theorem 5.3 tells us that \(e=0\) is asymptotically stable. Because we do not know the gain matrix \(K\) either, we need to jointly search for \(V\) and \(K\) (that are polynomials). Mathematically, this is \[\begin{equation} \begin{split} \text{find} & \quad V, K \\ \text{subject to} & \quad V(0) = 0, \quad V(e) > 0, \forall e \neq 0 \\ & \quad \dot{V}(e) = \frac{\partial V}{\partial e} \left( f(x + e) - f(x) + K(Ce,Cx)C e \right) < 0, \forall e \neq 0, \forall x \in \mathbb{X} \\ & \quad V(e) \geq \epsilon \Vert e \Vert^2, \forall e \end{split} \tag{6.83} \end{equation}\] where the last constraint is added to make sure \(V(e)\) is radially unbounded. Furthermore, if we replace the second constraint by \(\dot{V}(e) \leq - \lambda V(e)\), then we can guarantee \(V(e)\) converges to zero exponentially.

Problem (6.83), however, is not a convex optimization problem, due to the term \(\frac{\partial V}{\partial e} K\) being bilinear in the coefficients of \(V\) and \(K\). Nevertheless, as shown in (Ebenbauer, Renz, and Allgower 2005), we can use a reparameterization trick to formulate a stronger version of (6.83) as follows. \[\begin{equation} \begin{split} \text{find} & \quad V, Q(Ce), M(Ce,Cx) \\ \text{subject to} & \quad V(0) = 0, \quad V(e) > 0, \forall e \neq 0 \\ & \quad \frac{\partial V}{\partial e} = e^T Q(Ce), \quad Q(Ce) \succ 0 \\ & \quad e^T Q(Ce) \left( f(x + e) - f(x) \right) + e^T M(Ce,Cx) C e < 0, \forall e \neq 0, \forall x \in \mathbb{X} \\ & \quad V(e) \geq \epsilon \Vert e \Vert^2, \forall e \end{split} \tag{6.84} \end{equation}\] Clearly, if we can solve problem (6.84), then \[ K = Q(Ce)^{-1} M(Ce,Cx) \] is the right gain matrix for the formulation (6.83).

Let us bring this idea to action in our pendulum example.

Example 6.6 (Pendulum Observer with Convex Optimization) With \(x = [\mathfrak{s}, \mathfrak{c}, \dot{\theta}]^T\) (\(\mathfrak{s} = \sin \theta, \mathfrak{c} = \cos \theta\)), we can write the pendulum dynamics as \[ \dot{x} = \underbrace{\begin{bmatrix} \mathfrak{c} \dot{\theta} \\ - \mathfrak{s} \dot{\theta} \\ - \frac{b}{ml^2} \dot{\theta} \end{bmatrix}}_{=:f(x)} + \underbrace{\begin{bmatrix} 0 \\ 0 \\ \frac{u - mgl \mathfrak{s}}{ml^2} \end{bmatrix}}_{=: \psi(u,y)}, \quad y = \underbrace{\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \end{bmatrix}}_{=:C} x \] Clearly \(f(x)\) is a polynomial. Solving the convex optimization problem (6.84), we obtain a solution \[ V(e) = 0.5954 e_1^2 + 0.5954 e_2^2 + 0.9431 e_3^2 \] \[ Q(Ce) = \begin{bmatrix} 0.4603 e_2^2 + 1.1909 & -0.4603 e_1 e_2 & 0 \\ -0.4603 e_1 e_2 & 0.4603 e_1^2 + 1.1909 & 0 \\ 0 & 0 & 1.8863 \end{bmatrix} \] \[ M(Ce,Cx) = \begin{bmatrix} \substack{-2.0878 e_1^2 - 0.8667 e_2^2 - \\ 0.4588 (y_1^2 + y_2^2) - 0.4885} & - 0.8667 e_1 e_2 \\ - 0.8667 e_1 e_2 & \substack{-0.8667 e_1^2 - 2.0878 e_2^2 - \\ 0.4588 (y_1^2 + y_2^2) - 0.4885} \\ -1.1909 y_2 & 1.1909 y_1 \end{bmatrix} \]

Simulating this observer, we verify that the observer is in fact exponentially converging, as shown in Fig. 6.4.

The Matlab code for formulating and solving the convex optimization (6.84) can be found here. The code for simulating the observer can be found here.

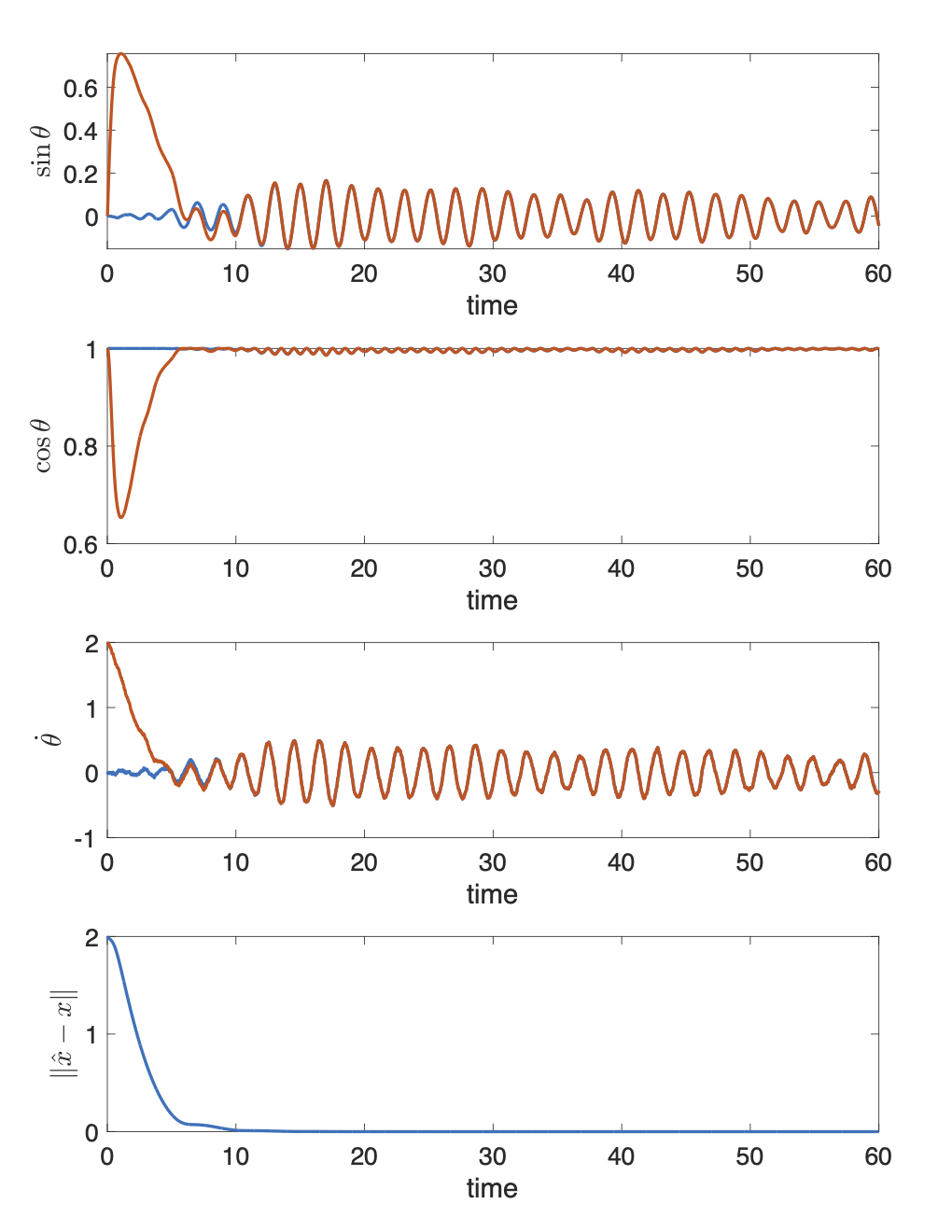
Figure 6.4: Simulation of the pendulum observer design from convex optimization

6.6 Observer Feedback

Now that we have good ways to design a state observer, we will see how we can use the observer for feedback control.

Example 6.7 (Pendulum Stabilization with A Luenberger Observer) In Example 6.3, we have written the dynamics of a pendulum, and the dynamics of a Luenberger observer as \[\begin{align} \dot{x} &= A x + B(u,y) \\ \dot{\hat{x}} &= A \hat{x} + B(u,y) + KC (x - \hat{x}) \end{align}\] We wish to understand (so we can optimize) the behavior of this system under certain control input \(u\). To do so, let us denote \(e = \hat{x} - x\), and write the above dynamics as \[\begin{align} \dot{x} &= A x + B(u,Cx) \\ \dot{e} & = (A - KC) e \end{align}\] Denoting \(z = [x,e]^T\), we have the augmented dynamics \[ \dot{z} = \underbrace{\begin{bmatrix} A & 0 \\ 0 & A - KC \end{bmatrix}}_{=:F} z + \underbrace{\begin{bmatrix} B(u,Dz) \\ 0 \end{bmatrix}}_{=:G(z,u)} \] We want to stabilize the system at \(z_0 = [\pi,0,0,0]^T\) (the upright position) subject to control bounds \(u \in \mathbb{U} = [-u_{\max},u_{\max}]\).

We need to find a control Lyapunov function (CLF), \(V(z)\), that satisfies the following constraints: \[ V(z_0) = 0 \] \[ V(z) > 0 \quad \forall z \in \{z: V(z) < \rho, z \neq z_0 \} \] \[ \inf_{u \in \mathbb{U}} [L_F V(z) + L_G V(z)] \leq 0 \quad \forall z \in \mathcal{Z} \]

where \(L_F V\) and \(L_G V\) are the Lie derivatives of \(V\) along \(F\) and \(G(z,u)\), respectively. \(\mathcal{Z}\) is the set of all possible augmented states. The CLF will define the set of admissible control inputs \(U\). \[ U = \{ u: L_f V(z) + L_g V(z)u \leq 0 \} \] To find the smallest-magnitude control input such that \(u \in K\), we may use a quadratic program:

\[ \min_{u \in \mathcal{U}} ||u||^2 \] \[ \mathrm{s.t.} \quad L_f V(z) + L_g V(z)u \leq -c V(z) \]

where \(c\) is some positive constant. The challenge now is in choosing a suitable \(V(z)\).

References

Andrieu, Vincent, and Laurent Praly. 2006. “On the Existence of a Kazantzis–Kravaris/Luenberger Observer.” SIAM Journal on Control and Optimization 45 (2): 432–56.

Astolfi, Alessandro, and Romeo Ortega. 2003. “Immersion and Invariance: A New Tool for Stabilization and Adaptive Control of Nonlinear Systems.” IEEE Transactions on Automatic Control 48 (4): 590–606.

Bernard, Pauline. 2019. Observer Design for Nonlinear Systems. Vol. 479. Springer.

Bernard, Pauline, Vincent Andrieu, and Daniele Astolfi. 2022. “Observer Design for Continuous-Time Dynamical Systems.” Annual Reviews in Control.

Besançon, Gildas, Guy Bornard, and Hassan Hammouri. 1996. “Observer Synthesis for a Class of Nonlinear Control Systems.” European Journal of Control 2 (3): 176–92.

Ebenbauer, Christian, Jonathan Renz, and F Allgower. 2005. “Polynomial Feedback and Observer Design Using Nonquadratic Lyapunov Functions.” In Proceedings of the 44th IEEE Conference on Decision and Control, 7587–92. IEEE.

Hammouri, Hassan, and Jesus de Leon Morales. 1990. “Observer Synthesis for State-Affine Systems.” In 29th IEEE Conference on Decision and Control, 784–85. IEEE.

Janny, Steeven, Vincent Andrieu, Madiha Nadri, and Christian Wolf. 2021. “Deep Kkl: Data-Driven Output Prediction for Non-Linear Systems.” In 2021 60th IEEE Conference on Decision and Control (CDC), 4376–81. IEEE.

Kalman, Rudolph E, and Richard S Bucy. 1961. “New Results in Linear Filtering and Prediction Theory.”

Kalman, Rudolph Emil. 1960. “A New Approach to Linear Filtering and Prediction Problems.”

Karagiannis, Dimitrios, and Alessandro Astolfi. 2005. “Nonlinear Observer Design Using Invariant Manifolds and Applications.” In Proceedings of the 44th IEEE Conference on Decision and Control, 7775–80. IEEE.

Kazantzis, Nikolaos, and Costas Kravaris. 1998. “Nonlinear Observer Design Using Lyapunov’s Auxiliary Theorem.” Systems & Control Letters 34 (5): 241–47.

Luenberger, David G. 1964. “Observing the State of a Linear System.” IEEE Transactions on Military Electronics 8 (2): 74–80.

Miao, Keyan, and Konstantinos Gatsis. 2023. “Learning Robust State Observers Using Neural ODEs.” In Learning for Dynamics and Control Conference, 208–19. PMLR.

Niazi, Muhammad Umar B, John Cao, Xudong Sun, Amritam Das, and Karl Henrik Johansson. 2023. “Learning-Based Design of Luenberger Observers for Autonomous Nonlinear Systems.” In 2023 American Control Conference (ACC), 3048–55. IEEE.

Reif, Konrad, Stefan Gunther, Engin Yaz, and Rolf Unbehauen. 1999. “Stochastic Stability of the Discrete-Time Extended Kalman Filter.” IEEE Transactions on Automatic Control 44 (4): 714–28.

Thrun, S, W Burgard, and D Fox. 2005. “Probabilistic Robotics.” MIT Press.

Van Der Merwe, Rudolph. 2004. Sigma-Point Kalman Filters for Probabilistic Inference in Dynamic State-Space Models. Oregon Health & Science University.

Yang, Tao, Prashant G Mehta, and Sean P Meyn. 2013. “Feedback Particle Filter.” IEEE Transactions on Automatic Control 58 (10): 2465–80.

---

8. We say “any solution” because there may be several solutions to the observer (6.52) due to \(\mathcal{F}\) only being continuous. This is not a problem as long as any such solution satisfies the required convergence property.↩︎

9. The time dependence of \(\mathcal{T}_u\) enables us to cover the case where the knowledge of the \(u\) and \(y_{x_0,u}\) is used to construct the estimate from the observer state. In particular, using the output sometimes can reduce the dimension of the observer state (and thus alleviate the computations), thus obtaining a reduced-order observer. For example, see (Karagiannis and Astolfi 2005) and (Astolfi and Ortega 2003).↩︎

10. A function \(\rho: \mathbb{R}_+ \rightarrow \mathbb{R}_+\) is a \(\mathcal{K}\) function if \(\rho(0) = 0\), \(\rho\) is continuous, and \(\rho\) is increasing.↩︎

11. An injective function is a function \(f\) that maps distinct elements of its domain to distinct elements. That is, \(f(x_a) = f(x_b)\) implies \(x_a = x_b\), or equivalently, \(x_a \neq x_b\) implies \(f(x_a) \neq f(x_b)\).↩︎

12. I have to say I was a bit surprised when I arrived at this formulation.↩︎